3.5.1. Questions
3.5.1.1. Minimum Area Rectangle
Given a set of distinct points in the xy-plane, determine the minimum area of a rectangle formed from these points, with sides parallel to the x and y axes.
If there isn't any rectangle, return 0.
Example 1:
Input: [[1,1],[1,3],[3,1],[3,3],[2,2]], Output: 4
Example 2:
Input: [[1,1],[1,3],[3,1],[3,3],[4,1],[4,3]], Output: 2
In this question, the sides of the rectangle must be parallel to the main axis, so we don’t have to consider a rotated rectangle. If we know the coordinates of the two diagonal vertices of the rectangle, it is very simple to find the area!
So we just need to find all the pair of points where their abscissa and ordinate are different.
In order to optimize the search time, the ordinates of all points with the same abscissa can be put into a HashSet in advance,
3.5.1.2. Relative Location
Given a string of two point names and coordinate position relationship, return whether there is such a position relationship (that is, whether there is a contradiction). The relationship could be one of: N, S, W, E, NE, NW, SE, SW.
Example:
Input: "1 NE 2, 2 SE 3, 3 W 1"
Output: true
Explanation:
3 1
2
point 1 is in the northeast of point 2, and point 2 is southeast of 3, point 3 is at the west side of point 1. It is spatially reasonable.
This is basically a graph problem.
1#include <gtest/gtest.h>
2
3#include <sein.hpp>
4
5namespace ns_relative_location {
6
7vector<string> split(string s) {
8 int p = 0;
9 vector<string> res;
10 while ((p = s.find(' ')) != string::npos) {
11 res.push_back(s.substr(0, p)), s = s.substr(p + 1);
12 }
13 if (!s.empty()) res.push_back(s);
14 return res;
15}
16
17static map<char, char> dirs = {{'N', 'S'}, {'S', 'N'}, {'W', 'E'}, {'E', 'W'}};
18
19string reverse_dir(string d) {
20 string r;
21 for (char c : d) r.push_back(dirs[c]);
22 return r;
23}
24
25bool dfs(map<string, map<string, string>>& graph, string x, string y, string& path) {
26 if (x == y) return true;
27 for (auto& [n, d] : graph[x]) {
28 string path_(path);
29 path += d;
30 if (dfs(graph, n, y, path)) return true;
31 path = path_;
32 }
33 return false;
34}
35
36string path_cross_out(string path) { // "NWSW" ==> "W"
37 vector<int> counter(123);
38 string res;
39 for (char c : path) counter[c]++;
40 auto tmp = counter;
41 for(auto c: {'N', 'S'})
42 counter[c] -= min(tmp['N'], tmp['S']);
43 for(auto c: {'W', 'E'})
44 counter[c] -= min(tmp['W'], tmp['E']);
45 for(auto c: {'N', 'S', 'W', 'E'})
46 if (counter[c]>0) res += c;
47 return res;
48}
49
50bool check_position(vector<string> v, string statement) {
51 map<string, pair<int, int>> m;
52 map<string, map<string, string>> graph;
53 for (string e : v) {
54 auto tr = split(e);
55 string a = tr[0], b = tr[1], c = tr[2];
56 graph[a][c] = b, graph[c][a] = reverse_dir(b);
57 }
58 auto stats = split(statement);
59 string x = stats[0], y = stats[2], x2y = stats[1];
60 string path;
61 dfs(graph, x, y, path);
62 string x2y_expected = path_cross_out(path);
63 return x2y == x2y_expected;
64}
65} // namespace ns_relative_location
66using namespace ns_relative_location;
67TEST(_relative_location, a) {
68 EXPECT_TRUE(check_position({"1 NE 2", "2 SE 3"},"3 W 1"));
69}
3.5.1.3. Edit Distance
Given two strings word1 and word2, return the minimum number of operations required to convert word1 to word2.
You have the following three operations permitted on a word:
Insert a character
Delete a character
Replace a character
Example 1:
Input: word1 = "horse", word2 = "ros"
Output: 3
Explanation:
horse -> rorse (replace 'h' with 'r')
rorse -> rose (remove 'r')
rose -> ros (remove 'e')
Example 2:
Input: word1 = "intention", word2 = "execution"
Output: 5
Explanation:
intention -> inention (remove 't')
inention -> enention (replace 'i' with 'e')
enention -> exention (replace 'n' with 'x')
exention -> exection (replace 'n' with 'c')
exection -> execution (insert 'u')
3.5.1.4. Fix Sentence
Given a sentence string and a dictionary. There are wrong words in the sentence while the correct words are in the dictionary. Can you correct the sentence with the dictionary with reasonable assumption?
Example
Input: Todxy is a god day.
Dictionary: {today, good}
Output: Today is a good day.
3.5.1.5. Max Points on a Line
Given n points on a 2D plane, find the maximum number of points that lie on the same straight line.
Example 1:
Input: [[1,1],[2,2],[3,3]]
Output: 3
Explanation:
^
|
| o
| o
| o
+------------->
0 1 2 3 4
Example 2:
Input: [[1,1],[3,2],[5,3],[4,1],[2,3],[1,4]]
Output: 4
Explanation:
^
|
| o
| o o
| o
| o o
+------------------->
0 1 2 3 4 5 6
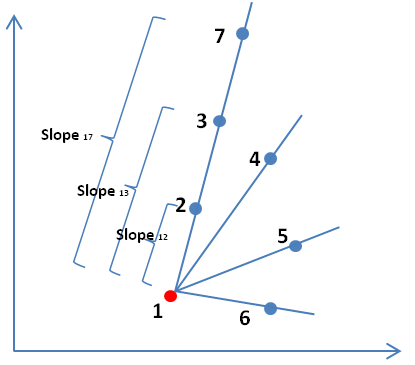
According to junior high school mathematics, it can be known that two points determine a straight line, and it can be written in the form of y = ax + b. All collinear points satisfy this formula. Therefore, a slope can be calculated between each pair of these given points. Each slope represents a straight line. For each straight line, bring in all the points to see if they are collinear and calculate the number. This is the basic idea.
However, there are two special cases to be considered. One is that when two points are duplicates, a straight line cannot be formed. The second is the case where the slope does not exist where their x coordinates are the same.
1struct Point { // Definition for a point
2 int x, y;
3 Point() : x(0), y(0) {}
4 Point(int a, int b) : x(a), y(b) {}
5};
6
7#define _equal(a, b) ((a.x == b.x) and (a.y == b.y))
8#define _slope(a, b) ((float)(a.y - b.y) / (a.x - b.x))
9
10struct Solution {
11 int maxPoints(vector<Point> &ps) { // T: O(N^2)
12 int r = 0, L = ps.size();
13 for (int i = 0; i < L; ++i) { // O(N^2)
14 int dup = 1;
15 unordered_map<float, int> counter;
16 counter[NAN] = 0;
17 for (int j = i+1; j < L; ++j) {
18 if (_equal(ps[i], ps[j]) and dup++) continue; // dup points
19 counter[ps[i].x == ps[j].x ? INFINITY : _slope(ps[i], ps[j])]++;
20 }
21 for (auto& [slope, count] : counter) r = max(r, count + dup);
22 }
23 return r;
24 }
25};
https://leetcode.com/problems/max-points-on-a-line/
👽 If we want to use drone for delivery, what can be done with ML?
3.5.1.6. Detect Squares
You are given a stream of points on the X-Y plane. Design an algorithm that:
Adds new points from the stream into a data structure. Duplicate points are allowed and should be treated as different points.
Given a query point, counts the number of ways to choose three points from the data structure such that the three points and the query point form an axis-aligned square with positive area.
An axis-aligned square is a square whose edges are all the same length and are either parallel or perpendicular to the x-axis and y-axis.
Implement the DetectSquares class:
- DetectSquares() Initializes the object with an empty data structure.
- void add(int[] point) Adds a new point point = [x, y] to the data structure.
- int count(int[] point) Counts the number of ways to form axis-aligned squares with point point = [x, y] as described above.
1#include <gtest/gtest.h>
2#include <sein.hpp>
3
4namespace ns_detect_square{
5class DetectSquares {
6map<pair<int,int>, int> m;
7public:
8DetectSquares() {}
9void add(vector<int> point) {
10 m[{point[0], point[1]}]++;
11}
12int count(vector<int> point) {
13 int x=point[0], y=point[1], res = 0;
14 for(auto [ps, count]: m){
15 auto [px, py] = ps;
16 if(px!=x and py!=y and m.count({x,py}) and m.count({px, y}))
17 res += m[ps]*m[{x,py}]*m[{px,y}];
18 }
19 return res;
20}
21};
22}
23using namespace ns_detect_square;
24TEST(_detect_square, a) {
25 DetectSquares ds;
26 vector<vector<int>> points={{3,10},{11,2},{3,2},{11,2}};
27 for(auto e: points) ds.add(e);
28 EXPECT_EQ(ds.count({11,10}), 2);
29}