3.2.1. Questions
3.2.1.1. Spiral Matrix
Print a matrix in spiral order
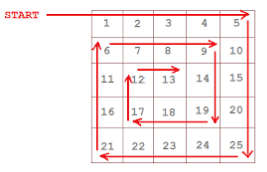
Solution:
1#include "sein.hpp"
2
3namespace matrix {
4struct Solution {
5 vector<int> spiralOrder(const vector<vector<int>> &m) {
6 vector<int> r;
7 if (m.empty() or m[0].empty()) return r;
8 int R = m.size(), C = m[0].size();
9 bool odd = (R & 1) or (C & 1);
10 for (int i = 0; i < (min(R, C) + (int)odd) / 2;
11 ++i) { // i+1 is the layer number which has been peeled
12 // i=0 is to peel the first layer
13 for (int j = i; j < C - i; ++j) r.push_back(m[i][j]);
14 for (int j = i + 1; j < R - 1 - i; ++j) r.push_back(m[j][C - 1 - i]);
15 if (R - 1 - i != i) {
16 for (int j = C - 1 - i; j >= i; --j) r.push_back(m[R - 1 - i][j]);
17 }
18 if (C - 1 - i != i) {
19 for (int j = R - 2 - i; j > i; --j) r.push_back(m[j][i]);
20 }
21 }
22 return r;
23 }
24};
25} // namespace matrix
3.2.1.2. Young Tableau
Sorted matrix can be considered as extension of sorted array, or a binary search tree with root in bottom left or top right corner. It is sorted not only in each row and column, but also in main diagonal.
3.2.1.3. Rotate Image/Matrix
3.2.1.4. Pascal Triangle
Solution:
1#include "sein.hpp"
2
3vector<vector<int>> generate(int numRows) {
4 vector<vector<int>> r(numRows, {1});
5 for (int i = 1, j; i < numRows; ++i) {
6 r[i].resize(i + 1);
7 for (j = 1; j < i; ++j)
8 r[i][j] = r[i - 1][j - 1] + r[i - 1][j];
9 r[i][j] = 1;
10 }
11 return r;
12}
you can use Spiral Matrix.
3.2.1.5. Minimum Time Interval
[Google Phone Screen] Given a string list, where each element in it is a timestamp, and the format is: "hh:mm", for example: ["23:23","11:13","21:01","01:03" ], returns the smallest time interval between two elements.
Algorithm time complexity should be better than O(NLogN).
We can use a 24x60 bool matrix as the bucket for bucket sort.
1namespace ns_bucket{
2int min_time_interval(vector<string> v){
3 vector<vector<bool>> bucket(24, vector<bool>(60));
4 for (string& s: v) {
5 int h = stoi(s.substr(0, 2)), m =stoi(s.substr(3,2));
6 if (bucket[h][m]) return 0;
7 bucket[h][m] = true;
8 }
9 int last=-1, r=INT_MAX;
10 for(int i=0;i<bucket.size();i++)
11 for(int j=0;j<bucket[0].size();j++)
12 if (bucket[i][j]){
13 int t=60*i + j;
14 if(last>0) r = min(r, t-last);
15 last = t;
16 }
17 return r;
18}
19}
20
21using namespace ns_bucket;
22TEST(_min_time_interval, a) {
23 vector<string> v = {"23:23","11:13","21:01","01:03"};
24 int r = min_time_interval(v);
25 EXPECT_TRUE(r == 142); // 2 hours 22 mins
26}
3.2.1.6. Minimum Flip
Given a matrix m with red(1) and blue(0) squares in it, you can only flip the top left square m[0][0] but there is a chain reaction, which is all the adjacent(up,down,left,right) squares of the same color are flipped accordingly.
Question: After how many flips, you can make all squares one color? Can you write a function to calculate it?
Example 1:
[0, 0, 1, 0] flip [1, 1, 1, 0] flip [0, 0, 0, 0] flip [1, 1, 1, 1]
[0, 1, 0, 1] -------> [1, 1, 0, 1] -------> [0, 0, 0, 1] -------> [1, 1, 1, 1]
[0, 1, 0, 1] [1, 1, 0, 1] [0, 0, 0, 1] [1, 1, 1, 1]
Output: 3
Example 2:
[0, 0, 1, 0] flip [1, 1, 1, 0] flip [0, 0, 0, 0]
[0, 0, 0, 1] -------> [1, 1, 1, 1] -------> [0, 0, 0, 0]
[0, 1, 0, 1] [1, 1, 1, 1] [0, 0, 0, 0]
Output: 2
Can you make your algorithm having time complexity: O(R*C)
1#include <gtest/gtest.h>
2#include <sein.hpp>
3
4namespace ns_min_flip {
5int get_min_flip(const vector<vector<int>> &m) {
6 if (m.empty() or m[0].empty()) return 0;
7 int R = m.size(), C = m[0].size();
8 vector<pair<int, int>> dirs = {{-1, 0},{1, 0}, {0, -1}, {0, 1}};
9 queue<pair<int, int>> q;
10 set<pair<int,int>> s, visited;
11 q.push({0, 0}), visited.insert({0, 0});
12 int count = 0;
13 while (not q.empty() or not s.empty()) {
14 while (!q.empty()) {
15 auto &[x, y] = q.front();
16 q.pop();
17 for (auto &[dx, dy]: dirs) {
18 int nx = x + dx, ny = y + dy;
19 if (0 <= nx and nx < R and 0 <= ny and ny < C and not visited.count({nx, ny})) {
20 if (m[nx][ny] == m[x][y]) {
21 q.emplace(nx, ny), visited.insert({nx, ny});
22 } else {
23 s.emplace(nx, ny);
24 }
25 }
26 }
27 }
28 for(auto &i: s) q.push(i), visited.insert(i);
29 s.clear(), count++;
30 }
31 return count-1;
32}
33}
34using namespace ns_min_flip;
35TEST(_ns_min_flip, a) {
36 vector<vector<int>> m;
37 m = {{0, 0, 1, 0},
38 {0, 1, 0, 1},
39 {0, 1, 0, 1}};
40 EXPECT_TRUE(get_min_flip(m) == 3);
41 m = {{0, 0, 1, 0},
42 {0, 0, 0, 1},
43 {0, 1, 0, 1}};
44 EXPECT_TRUE(get_min_flip(m) == 2);
45 m = {{0, 1, 0, 1},
46 {1, 0, 1, 0},
47 {0, 1, 0, 1}};
48 EXPECT_TRUE(get_min_flip(m) == 5);
49 m = {{1, 0, 1, 1},
50 {1, 0, 0, 0},
51 {1, 1, 1, 1}};
52 EXPECT_TRUE(get_min_flip(m) == 2);
53 m = {{0}};
54 EXPECT_TRUE(get_min_flip(m) == 0);
55 m = {{1}};
56 EXPECT_TRUE(get_min_flip(m) == 0);
57 m = {{1, 1, 1}};
58 EXPECT_TRUE(get_min_flip(m) == 0);
59}