3.3.3. Segment Tree

A Segment Tree is a data structure that allows answering range queries over an array effectively, while still being flexible enough to allow modifying the array.

Features of Segment trees:

1. Leaf Nodes are the elements of the input array. This is like tournament tree described at Section 3.3.4.

2. Each internal node represents some merging of the leaf nodes. The merging may be different for different problems. If we want to query minimum value of a range, merging is minimum of leaves under a node.

3.3.3.1. Subarray Minimum Query

There are many ways to implement a segement tree. The following is an example to build a minimum segement tree using vector as the underlying data strucutre.

class segment_tree_min {
public:
  explicit segment_tree_min(const vector<int> &values) {
    n = values.size();
    data = vector<int>(2 * n);
    copy(values.begin(), values.end(), &data[0] + n);
    // fill segment tree inner nodes
    for (int idx = n - 1; idx > 0; idx--)
      data[idx] = min(data[idx * 2], data[idx * 2 + 1]);
  }

  void update(int idx, int value) {
    // update original data
    idx += n;
    data[idx] = value;
    // populate from bottom to top
    while (idx > 1) {
      idx >>= 1;
      data[idx] = min(data[2 * idx], data[2 * idx + 1]);
    }
  }

  int query(int left, int right) { // interval [left, right)
    int ret = numeric_limits<int>::max();
    left += n, right += n;
    while (left < right) {
      if (left & 1) // odd index
        ret = min(ret, data[left++]);
      if (right & 1) // odd index
        ret = min(ret, data[--right]);
      left >>= 1, right >>= 1;
    }
    return ret;
  }

private:
  int n; // size of the original data
  vector<int> data; // base data structure is a vector
};

In the above implementation, we deliberately don’t use the first item in the underlying vector. So the node at array[index] has its children at array[index*2] and array[index*2+1]. The node at array[index] has its parent at array[index/2]. [1]

If the original array is {5,2,3,1,4}. First we copy all the array to the second part of the underlying vector. Then we populate the inner nodes.

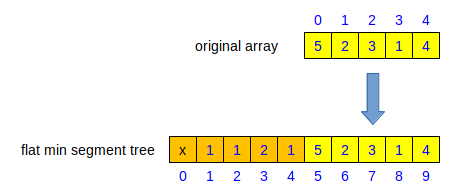
Figure 3.3.1 Segment Tree Indexing Scheme

Finally we will get a segment tree as a full binary tree [2].

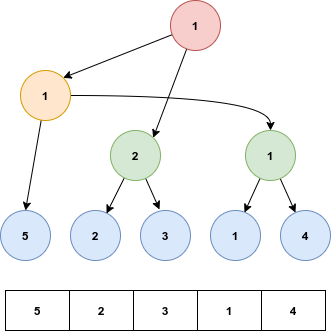
Figure 3.3.2 Construct Segment Tree

           [2]
        /       \
      [2]      [4]
      /   \     /  \
data [2]  [3]  [4] [5]

original index: [0][1][2][3]
original array: [2][3][4][5]
index: [x][1][2][3][4][5][6][7]   (tree index)
value: [x][2][2][4][2][3][4][5]   (tree)

input 0,3 => 4, 7

                 [2]
               /  /
           [2]---/---
          /     /    \
       [2]   [2]     [5]
       /    /   \   /  \
data [2]  [3]  [4] [5] [6]

To make the tree easier to see, we can adjust it like:

Figure 3.3.3 Segment Tree As Full Binary Tree

The tricky part is the query function, where we need to check if the upper level’s parent node has the left-most or right-most node as a child. If not, we need to add the left-most or right-most node into the calculation.

Footnotes

[1]

A full binary tree (sometimes proper binary tree or 2-tree) is a tree in which every node other than the leaves has two children. Heap is complete binary tree. None of them are not necessarily perfect binary tree.

[2]

The indexing scheme is different from what described for 0-index-based heap. For heap, the item at array[index] has its children at array[index*2+1] and array[index*2+2]. The node at array[index] has its parent at array[(index-1)/2].

3.3.3.2. Buddy System Bitmap

class segment_tree_bitmap {
  long long tree_size;  // even number always
  vector<bool> flat_stree;

  void build(long long n) {
    flat_stree.resize(2 * n);  // all false when initialization
    tree_size = 2 * n;
  }

  void update(long long tree_index, bool b) {  // bottom up, TC: O(LogN)
    flat_stree[tree_index] = b;
    long long i = tree_index;
    while (i > 0) {
      if (i & 1) {
        flat_stree[i >> 1] = flat_stree[i] & flat_stree[i - 1];
      } else {
        flat_stree[i >> 1] = flat_stree[i] & flat_stree[i + 1];
      }
      i /= 2;
    }
  }

 public:
  explicit segment_tree_bitmap(long long n) { build(n); }

  long long allocate() {           // top down, TC: O(LogN)
    if (flat_stree[1]) return -1;  // capacity is full
    long long i = 1, j = 2;        // i - parent, j - left child
    // 1. find tree_index to update
    while (j < tree_size) {
      if (i & 1) {
        if (flat_stree[j]) j++;
      } else {
        if (j + 1 < tree_size and !flat_stree[j + 1]) j++;
      }
      i = j, j = i << 1;
    }
    long long tree_index = i;
    // 2. update
    update(tree_index, true);
    return tree_index - tree_size / 2;
  }

  bool release(long long n) {  // TC: O(LogN)
    long long tree_index = n + tree_size / 2;
    if (!flat_stree[tree_index]) return false;
    update(tree_index, false);
    return true;
  }
};

• heap tree indexing scheme