2.6.1. General Binary Search Tree
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
explicit TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
typedef TreeNode BTNode;
struct BTPNode {
int val;
BTPNode *left;
BTPNode *right;
BTPNode *parent;
explicit BTPNode(int x) : val(x), left(NULL), right(NULL), parent(NULL) {}
};
2.6.1.1. Validate Binary Search Tree
Given a binary tree, determine if it is a valid binary search tree (BST).
Assume a BST is defined as follows: The left subtree of a node contains only nodes with keys less than the node’s key. The right subtree of a node contains only nodes with keys greater than the node’s key. Both the left and right subtrees must also be binary search trees.
Note we don’t consider duplicate key since this is a strictly monotonically increasing BST.
Recursion
1bool is_bst_recursive(TreeNode* root, TreeNode* mi = 0, TreeNode* mx = 0) {
2 if (!root) return 1;
3 if (mi && mi->val >= root->val) return false;
4 if (mx && mx->val <= root->val) return false;
5 return is_bst_recursive(root->left, mi, root) and
6 is_bst_recursive(root->right, root, mx);
7}
Iterative in-order traversal with stack
Another method is to traverse the BST in order, and check if the resulting sequence is monotonically increasing. The implementation may be tricky. A good way to avoid losing track is to compare your implementation’s stack with the DFS stack, assuming you are doing DFS(depth first search).
1bool is_bst_iterative(TreeNode* c) {
2 stack<TreeNode*> stk;
3 long long tmp = INT_MIN - 1L; // L is important
4 while (!stk.empty() or c) {
5 while (c) stk.push(c), c = c->left;
6 if (tmp != INT_MIN - 1L and tmp >= stk.top()->val) return false;
7 tmp = stk.top()->val, c = stk.top()->right, stk.pop();
8 }
9 return true;
10}
Morris traversal
1bool is_bst_morris(TreeNode* c) {
2 long long prev = INT_MIN - 1L;
3 while (c) {
4 if (c->left) {
5 TreeNode* p = c->left;
6 while (p->right) p = p->right;
7 p->right = c;
8 TreeNode* tmp = c;
9 c = c->left, tmp->left = 0;
10 } else {
11 if (prev != INT_MIN - 1L && prev >= c->val) return false;
12 prev = c->val;
13 c = c->right;
14 }
15 }
16 return 1;
17}
2.6.1.2. Minimum Distance Between BST Nodes
Given a Binary Search Tree (BST) with the root node root, return the minimum difference between the values of any two different nodes in the tree.
Example :
Input: root = [4,2,6,1,3,null,null]
Output: 1
Explanation:
Note that root is a TreeNode object, not an array.
The given tree [4,2,6,1,3,null,null] is represented by the following diagram:
4
/ \
2 6
/ \
1 3
while the minimum difference in this tree is 1, it occurs between node 1 and node 2, also between node 3 and node 2.
2.6.1.3. Inorder Successor in BST
Given a binary search tree and a node in it, find the in-order successor of that node in the BST.
Function Signature:
// return in-order successor of p
TreeNode* inorderSuccessor(TreeNode* root, TreeNode* p)
Note: If the given node has no in-order successor in the tree, return null.
This question asks us to find the in-order successor node of a node in the binary search tree. According to the nature of BST, we know that the result of its in-order traversal is sorted. The naive method is to use iterative in-order traversal. We can use a bool-type variable b, initialized to false, and perform in-order traversal. For the traversed node, first see if b is already true at this time, indicating that p has been traversed before, then return the current node as the result. If b is false, check if the traversed node is the same as p, if it is, assign b to true, then the next traversed node can be returned. The time complexity will be O(N) where N is the number of the tree nodes.
Let’s look at a even simpler method. This method makes full use of the properties of BST and time complexity is O(H) where H is height of the tree.
2.6.1.3.1. Node Without Parent Pointer
First, look at the root node value and the p node value. If the root node value is large, it means that the p node must be in the left subtree, then the result is firstly assigned to root. Then root is moved to its left child node. The condition of the loop is that root exists, and then compare the root value and the p node value. If the root value is still large, repeat the above operation. Otherwise, move root to its right child node, so that when root is empty, result points to the successor node of p, see the code as Code Block 2.6.6.
1TreeNode *inorderSuccessor_iter(TreeNode *root, TreeNode *p) {
2 TreeNode *result = NULL;
3 while (root) {
4 if (root->val > p->val) {
5 result = root;
6 root = root->left;
7 } else
8 root = root->right;
9 }
10 return result;
11}
The above method can also be written in recursive form, and it is relatively simple. When the value of the root node is less than or equal to the value of the p node, it means that the successor node of p must be in the right subtree, so the right child node is used in the recursive function. If the value of the root node is greater than the value of the p node, it is possible that the root node itself is the successor node of p, or a node in its left subtree is the successor node of p. Therefore, firstly we recursively call this function on the left child node. If it returns a non-empty node, just return that node. If it returns empty, it means that the root node itself is the successor node, we can return it. See the code as Code Block 2.6.7.
1TreeNode *inorderSuccessor_rec(TreeNode *root, TreeNode *p) {
2 if (!root) return NULL;
3 if (root->val <= p->val) {
4 return inorderSuccessor(root->right, p);
5 } else {
6 TreeNode *left = inorderSuccessor(root->left, p);
7 return left ? left : root;
8 }
9}
2.6.1.3.2. Node With Parent Pointer
When there is a parent pointer in the node, we don’t even need the root parameter in the function. We just need the node itself. In Figure 2.6.2, the successor of node a is node f, and the successor of node b is node i.
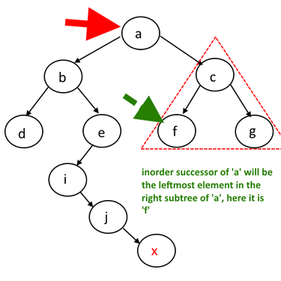
Figure 2.6.2 Node With Parent Pointer Case 1
In Figure 2.6.3, the successor of node x is node e.
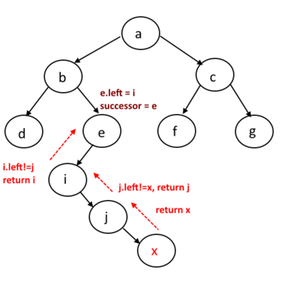
Figure 2.6.3 Node With Parent Pointer Case 2
1struct node * inOrderSuccessor(TreeNode *n){
2 // 1. move downward if there is right child
3 if( n->right ) return minValue(n->right);
4 // 2. otherwise, go up
5 struct node *p = n->parent;
6 while(p && n == p->right)
7 n = p, p = p->parent;
8 return p;
9}
Note we neither look up any of the node’s value, nor the left child pointer.
2.6.1.4. Median Binary Tree
Median is the middle value in an ordered integer list. If the size of the list is even, there is no middle value, so the median is the mean of the two middle values.
Design a data structure that supports the following two operations:
void addNum(int num) - Add a integer number from the data stream to the data structure.
double findMedian() - Return the median of all elements so far.
For example:
add(1)
add(2)
findMedian() -> 1.5
add(3)
findMedian() -> 2
This solution uses an ordinary binary tree for simplicity’s sake, which means it is likely to be unbalanced. Given enough time one may well use a balanced binary tree implementation to guarantee O(logn) runtime for addNum(). It is easy to see that findMedian() runs in O(1).
By using a binary tree, we can easily keep the input numbers in nondecreasing order. Observe that whenever a number is added, the numbers used to calculate the median never shift by more than 1 position (in an imagined array representation) to the left or to the right. Let’s see an example: [2], number used to calculate median is 2. [2,3], numbers used are 2,3 (expanding 1 to right) [0,2,3], use 2 (shrinking 1 to left) [0,1,2,3], use 1,2 (expanding 1 to left) [0,1,2,3,4], use 2 (shrinking 1 to right) ….and so on.
With this observation, in MedianFinder we employ 2 variables medianLeft and medianRight to keep track of numbers we need to calculate the median. When size is odd, they point to the same node, otherwise they always point to 2 nodes which have predecessor/successor relationship. When adding a node, we just need to check the size of our MedianFinder tree, then depending on whether the new number is inserted to the left, in-between, or to the right of our 2 median trackers, we will change medianLeft and medianRight to point to the correct nodes. Because the position never shifts more than 1, we can simply use predecessor() or successor() on the desired node to update it. Those 2 methods run in O(logn) when the tree is balanced, hence the O(logn) runtime of addNum().