2.4. Priority Queue
Priority queue is a weighted queue. Since it is a queue, it allows you to add, delete, and peek element, but nothing else. In most cases, priority queue is implemented as a binary heap tree. Heap tree is complete tree, so the index can be calculated if all the nodes are stored in a sequential array. (Complete means there is no hole inside the tree.)
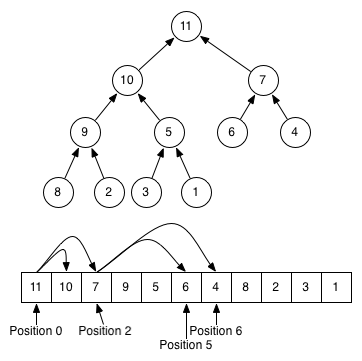
Figure 2.4.1 A max binary heap tree stored a flat array
In C++, a 0-based array is used as the underlying data structure, the indexing scheme is:
1#define PAR(i) ((i - 1) >> 1) // (i-1)/2, parent index macro
2#define LEF(i) ((i << 1) + 1) // 2i+1, left child index
3#define RIG(i) ((i << 1) + 2) // 2i+2, right child index
If parent node index is i, left child index is 2i+1, and right child index is 2i+2. If child index is i, the parent index is (i-1)/2. (Refer to how segement tree makes this easier at Section 3.3.3.1)
Heap Node Comparator
Unlike map or set, defining a less-than operator< inside the object class doesn’t work for priority_queue. You need to use a separate comparator class with an operator() method.
1struct comp{ // a min heap comparator
2 bool operator()(const Node* a, const Node* b){return a->key > b->key;}
3};
This way you have to use the comparator as a template argument when declaring the priority queue.
1 priority_queue<Node*, vector<Node*>, comp> pq; // min heap
There are other ways like using lambda, or overload the less-than operator globally.
🐾 The time complexity of building a heap is linear!
The following are a list advanced algorithms or applications using priority queue:
Beam Search
Heavy Hitters(top-k problem)
K-way Merge
Dijkstra algorithm for weighted graph
Huffman Coding
Prim’s Algorithm
Job scheduling and interrupt handling.
Heap seems very similar to segment tree, but actually they are very different. All heap nodes are from input. For segment tree, only leaves are from input, and inner nodes are result of computing.
Another data structure similar to heap is Young Tableau.