2.3.1. Questions

2.3.1.1. Linked List Cycle

• Given a linked list, determine if it has a cycle in it.

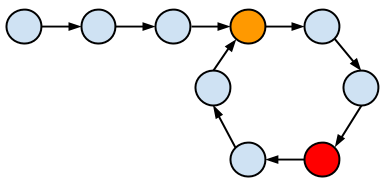
Figure 2.3.1 Use Floyd’s Tortoise And Hare Algorithm To Detect Cycle

  bool hasCycle(ListNode *head) {
      ListNode *slow=head, *fast=head;
      while(fast && fast->next){ // dont have to check slow
          slow=slow->next;
          fast=fast->next->next;
          if(slow==fast) return true;
      }
      return false;
  }

• Given a linked list, return the node where the cycle begins, like node Y in Figure 2.3.2. If there is no cycle, return null.

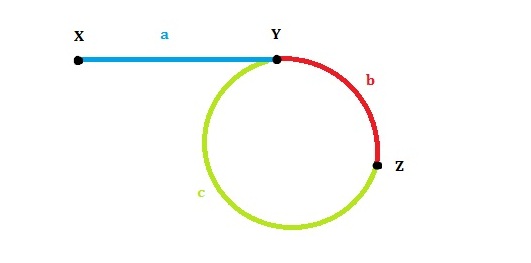
Figure 2.3.2 Find Where The Cycle Begins

Proof: The tortoise moves d = a + b + N L , hare moves two times as tortoise 2 d = a + b + M L , so d = ( M − N ) L = a + b + N L , and a + b = ( M − 2 N ) L . M − 2 N is an positive integer. So at point Z, if tortoise moves a step, it will get point Y. a is not necessarily equal to c, but what we can guarantee is that starting from Z, one will reach Y after a steps(although it is possible that one has circled for several rounds).

ListNode *detectCycle(ListNode *head) {
    if (!head || !head->next) return nullptr;//
    ListNode *t=head, *h=head; // t is tortoise and h is hare
    while(h && h->next){
        t=t->next, h=h->next->next;
        if(t==h) break;
    }
    if(t!=h) return 0;
    t=head; // put tortoise back to the list head
    while(t != h)
        t=t->next, h=h->next;
    return t; // When they meet again, it is at point Y
}

2.3.1.2. Linked List Random Node

Given a singly linked list, return a random node’s value from the linked list. Each node must have the same probability of being chosen.

Follow up: What if the linked list is extremely large and its length is unknown to you? Could you solve this efficiently without using extra space?

This is related to Reservoir Sampling.

class Solution {
  ListNode *head;
public:
  Solution(ListNode* head) :head(head) {}
  int getRandom() {
    int ans = 0;
    ListNode *p = head;
    for (int cnt = 1; p; cnt++, p = p->next)
      if (rand() % cnt == 0)
        ans = p->val;
    return ans;
  }
};

2.3.1.3. Merge K Sorted Lists

Merge k sorted linked lists and return it as one sorted list. Analyze and describe its complexity.

---

TC: O(NlogK), SC: O(K) where N is total number of Nodes and K is number of lists

class Solution {
    struct comp{ // comparator for min-heap
        bool operator () (ListNode* lhs, ListNode* rhs){
          return lhs->val > rhs->val;
        }
    };
public:
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        if(lists.size() == 0) return nullptr;
        ListNode dummy(-1);
        ListNode *p = &dummy;
        priority_queue<ListNode*,vector<ListNode*>,comp> pq;
        for(ListNode *head : lists)
            if(head != nullptr) pq.push(head);
        while(!pq.empty()){
            ListNode* node = pq.top(); pq.pop();
            p->next = node;
            if(node->next != nullptr)
                pq.push(node->next);
            p = p->next;
        }
        return dummy.next;
    }
};

2.3.1.4. Tweets Diversification

Given a list of tweets sorted by scores descendingly with their corresponding scores and authors, transform the list such that consecutive tweets cannot be from the same author whenever possible. Always prefer the author whose tweets have the highest score if there are multiple possible authors to be considered.

Conditions: 0.0 < Score <= 1.0

Each tuple (score, authorId) represents a tweet. Input is a list of tweets with authors ranked in some initial ordering. The output is a list of tweets such that tweets by the same author are not together.

Example 1
Input: rankedTweetList = [(.6, "A"), (.5, "A"), (.4, "B"), (.3, "B"), (.2, "C"), (.1, "C")]
Output:rankedTweetListAfterDiversity = [(.6, "A"), (.4, "B"), (.5, "A"), (.3, "B"), (.2, "C"), (.1, "C")]

Example 2
Input: rankedTweetList = [(.5, "A"), (.4, "A"), (.3, "A"), (.2, "B"), (.1, "A")]
Output: rankedTweetListAfterDiversity = [(.5, "A"), (.2, "B"), (.4, "A"), (.3, "A"), (.1, "A")]

vector<pair<double, char>> reorder(vector<pair<double, char>> tweets){
  list<pair<double, char>> extra;
  vector<pair<double, char>> result;
  for(int i=0;i<tweets.size();i++){
    if (result.empty()){
      result.push_back(tweets[i]);
      continue;
    }
    if(result.back().second == tweets[i].second){
      extra.push_back(tweets[i]); // add 5A into extra list
    }else{ // 4B
      result.push_back(tweets[i]); // 6A 4B
      if(not extra.empty() and result.back().second != extra.front().second){ //
        result.push_back(extra.front()); // 6A 4B 5A
        extra.erase(extra.begin());
      }
    }
  }
  for(auto i: extra) result.push_back(i);
  return result;
}

👽 Follow up: how to make the result as diverse as possible?

Data Structure:
- heap tree (weight, as meidan+.001*number of tweets, other metrics) + map
- round-robin map

// A -> 0.6, 0.5
// B -> 0.4
// C -> 0.5,0,3
// D -> 0.00002

- kv cache like redis
- LRU cahce read/written by app server