3.8.9. Questions
3.8.9.1. Babyfaces And Heels
There are 2 types of professional wrestlers: babyfaces and heels. Between any pair of professional wrestlers, there may or may not be a rivalry. Suppose we have n professional wrestlers and we have a list of r pairs of wrestlers for which there are rivalries. Write a function to determines whether it is possible to designate some of the wrestlers as babyfaces and the remainder as heels such that each rivalry is between a babyface and a heel.
For example:
Given n = 5 and 5 pairs of wrestlers: {{0, 1}, {0, 2}, {0, 3}, {1, 4}, {3, 4}}, return true.
Given n = 5 and 5 pairs of wrestlers: {{0, 1}, {0, 2}, {0, 3}, {1, 4}, {2, 3}}, return false.
3.8.9.2. Is Graph A Valid Tree?
Given n nodes labeled from 0 to n - 1 and a list of undirected edges (each edge is a pair of nodes), write a function to check whether these edges make up a valid tree.
For example:
Given n = 5 and edges = {{0, 1}, {0, 2}, {0, 3}, {1, 4}}, return true.
Given n = 5 and edges = {{0, 1}, {1, 2}, {2, 3}, {1, 3}, {1, 4}}, return false.
3.8.9.3. Walls and Gates
You are given a m x n 2D grid initialized with these three possible values.
-1 - A wall or an obstacle.
0 - A gate.
INF - Infinity means an empty room. We use the value 2^{31} - 1 = 2147483647 to represent INF as you may assume that the distance to a gate is less than 2147483647.
Fill each empty room with the distance to its nearest gate. If it is impossible to reach a gate, it should be filled with INF.
For example, given the 2D grid:
INF -1 0 INF
INF INF INF -1
INF -1 INF -1
0 -1 INF INF
After running your function, the 2D grid should be:
3 -1 0 1
2 2 1 -1
1 -1 2 -1
0 -1 3 4
This is a simple version of multi-source-BFS problem. It is simple because the graph is clear, which is made of all INF nodes, and you can mark it to a non-INF value so you don’t have to maintain a visited set for nodes that has been traversed. This graph is changed when tracersing so that you can’t go back to traverse the same node again.
1void walls_gates(vector<vector<int>>& rooms) {
2 if (rooms.empty() or rooms[0].empty()) return;
3 int INF = 0x7fffffff, R = rooms.size(), C = rooms[0].size();
4 const array<pair<int, int>, 4> dirs{{{-1, 0}, {0, -1}, {0, 1}, {1, 0}}};
5 queue<pair<int, int>> q;
6 for (int i = 0; i < R; ++i)
7 for (int j = 0; j < C; ++j)
8 if (0 == rooms[i][j]) q.push({i, j});
9 while (!q.empty()) {
10 pair<int, int> h = q.front();
11 q.pop();
12 int x(h.first), y(h.second);
13 for (int k = 0; k < dirs.size(); ++k) {
14 int nx(x + dirs[k].first), ny(y + dirs[k].second);
15 if (0 <= nx and nx < R and 0 <= ny and ny < C and rooms[nx][ny] == INF)
16 rooms[nx][ny] = rooms[x][y] + 1, q.push({nx, ny});
17 }
18 }
19}
3.8.9.4. Word Ladder
Given two words (beginWord and endWord), and a dictionary’s word list, find the length of shortest transformation sequence from beginWord to endWord, such that:
Only one letter can be changed at a time. Each transformed word must exist in the word list. Note that beginWord is not a transformed word.
For example, given: beginWord = “hit”, endWord = “cog”, wordList = {“hot”,“dot”,“dog”,“lot”,“log”,“cog”}. As one shortest transformation is “hit” -> “hot” -> “dot” -> “dog” -> “cog”, return its length 5.
Note:
Return 0 if there is no such transformation sequence.
All words have the same length.
All words contain only lowercase alphabetic characters.
No duplicates in the word list.
You may assume beginWord and endWord are non-empty and are not the same.
This solution is fast because:
Bidirectional-BFS
No graph building, just finding neighbours on the fly.
No visited set, just reusing wordList and erasing visited node from it
Another version which uses int in the unordered set.
3.8.9.5. Word Ladder II
Given two words (beginWord and endWord), and a dictionary’s word list, find all shortest transformation sequence(s) from beginWord to endWord, such that:
Only one letter can be changed at a time
Each transformed word must exist in the word list. Note that beginWord is not a transformed word.
For example, given: beginWord = “hit”, endWord = “cog”
wordList = {“hot”,“dot”,“dog”,“lot”,“log”,“cog”}
Return
{
{“hit”,“hot”,“dot”,“dog”,“cog”},
{“hit”,“hot”,“lot”,“log”,“cog”}
}
Note:
Return an empty list if there is no such transformation sequence.
All words have the same length.
All words contain only lowercase alphabetic characters.
You may assume no duplicates in the word list.
You may assume beginWord and endWord are non-empty and are not the same.
There are two steps to solve this problem. First,
3.8.9.6. Expression Add Operators
Given a string that contains only digits 0-9 and a target value, return all possibilities to add binary operators (not unary) +, -, or * between the digits so they evaluate to the target value.
Examples:
"123", 6 -> {"1+2+3", "1*2*3"}
"232", 8 -> {"2*3+2", "2+3*2"}
"105", 5 -> {"1*0+5","10-5"}
"00", 0 -> {"0+0", "0-0", "0*0"}
"3456237490", 9191 -> {}
3.8.9.7. Course Schedule
There are a total of n courses you have to take, labeled from 0 to n - 1. Some courses may have prerequisites, for example to take course 0 you have to first take course 1, which is expressed as a pair: {0,1}
Given the total number of courses and a list of prerequisite pairs, is it possible for you to finish all courses?
For example:
2, {{1,0}}
There are a total of 2 courses to take. To take course 1 you should have finished course 0. So it is possible.
2, {{1,0},{0,1}}
There are a total of 2 courses to take. To take course 1 you should have finished course 0, and to take course 0 you should also have finished course 1. So it is impossible.
Note:
The input prerequisites is a graph represented by a list of edges, not adjacency matrices. Read more about how a graph is represented.
You may assume that there are no duplicate edges in the input prerequisites.
Hints:
1. This problem is equivalent to finding if a cycle exists in a directed graph. If a cycle exists, no topological ordering exists and therefore it will be impossible to take all courses.
2. There are several ways to represent a graph. For example, the input prerequisites is a graph represented by a list of edges. Is this graph representation appropriate?
3. Topological Sort via DFS - A great video tutorial (21 minutes) on Coursera explaining the basic concepts of Topological Sort.
4. Topological sort could also be done via BFS.
The question reminds me of my college life. When choosing a course, we often encounter that we want to choose a certain course, but find out which courses must be taken before choosing it. This question gives a lot of hints, The first one tells that the essence of this problem is to detect cycles in a directed graph. The second hint is about how to represent a directed graph, which can be represented by an edge, and an edge is represented by two points. The third and fourth hints reveal that there are two solutions to this problem, both DFS and BFS can solve this problem.
Let’s first look at the solution of BFS.
BFS
In course_schedule_bfs, we first define a two-dimensional vector graph to represent this directed graph, and a one-dimensional vector in to represent the in-degree of each vertex. Then we start to build this directed graph based on the input, and initialize the in-degree array as well.
Then define a queue variable, put all the points whose in-degree is 0 into the queue, and then start looping through the queue. For each vertex popped out from the queue, we decrease the in-degree of the connected vertex in the graph by 1. If the connected vertex’s in-degree becomes 0, it is enqueued at the end of the queue. When all the vertices in the queue are popped out, if there is still any non-zero in-degree vertex in the graph, it means that circle exists and then we returns false. Otherwise, we returns true.
topologically sortable == No cycle!
Kahn Algorithm
Kahn’s algorithm is a more generic solution based on BFS. We need a successor graph and a predecessor graph, and a set with all vertices. Note we’ve never used numCourses in the function in course_schedule_kahn.
Find 0-indegree node: delete the key of pre from ns, ns==[a], which contains 0-indegree nodes(‘a’ in this case).
Then remove all a nodes from pre and suc : First check suc, look for points b, c, f in suc[a], then look for pre[b], pre[c], pre[f], which must all contain a, delete this a, if there is any left The next is an empty set, indicating that another 0-indegree node is found.
Repeat until ns is empty!
Finally, if pre and suc are also empty, it means that it is topologically sortable!!! In this process, all the nodes have been found in order. node, in another words, we have done topological sort.
Postorder DFS
Let’s look at the solution of DFS. We also need to build a directed graph using a two-dimensional vector. Unlike BFS, a one-dimensional vector visit is used to track the vertex state. A vertex has three states in DFS: 0 means undiscovered, 1 means finished, -1 means discovered. The basic idea is to build a directed graph first, then start from the first course, find which course we can take after the first course, temporarily mark the current course as discovered, and then call DFS recursively on the newly obtained course. If a new course has status discovered, return false because discovering a course two times means a circle is detected. If it has status finished, return true.
Complexity
3.8.9.8. Course Schedule II
There are a total of n courses you have to take, labeled from 0 to n - 1. Some courses may have prerequisites, for example to take course 0 you have to first take course 1, which is expressed as a pair: {0,1}
Given the total number of courses and a list of prerequisite pairs, return the ordering of courses you should take to finish all courses. If there are many valid answers, return any of them. If it is impossible to finish all courses, return an empty array.
Example:
Input: numCourses = 4, prerequisites = [[1,0],[2,0],[3,1],[3,2]]
Output: [0,2,1,3]
Explanation: There are a total of 4 courses to take. To take course 3 you should have finished both courses 1 and 2. Both courses 1 and 2 should be taken after you finished course 0. So one correct course order is [0,1,2,3]. Another correct ordering is [0,2,1,3].
👽 follow up - find all feasible solutions:
// Construct predecessor subgraph and BFTree
vector<vector<int>> r;
while (!Q.empty()) {
int count = Q.size();
vector<int> p;
while (--count) {
int t = Q.front(); Q.pop();
p.push_back(t);
for (int i : G[t]) { if (--in[i] == 0) Q.push(i); }
}
r.push_back(p);
}
// DFS to find all paths
Refer to Section 3.7.1.
3.8.9.9. Reconstruct Itinerary
Given a list of airline tickets represented by pairs of departure and arrival airports {from, to}, reconstruct the itinerary in order. All of the tickets belong to a man who departs from JFK. Thus, the itinerary must begin with JFK.
Note:
If there are multiple valid itineraries, you should return the itinerary that has the smallest lexical order when read as a single string. For example, the itinerary {“JFK”, “LGA”} has a smaller lexical order than {“JFK”, “LGB”}. All airports are represented by three capital letters (IATA code). You may assume all tickets form at least one valid itinerary.
Example 1:
tickets = {{"MUC", "LHR"}, {"JFK", "MUC"}, {"SFO", "SJC"}, {"LHR", "SFO"}}
Return {"JFK", "MUC", "LHR", "SFO", "SJC"}.
Example 2:
tickets = {{"JFK","SFO"},{"JFK","ATL"},{"SFO","ATL"},{"ATL","JFK"},{"ATL","SFO"}}
Return {"JFK","ATL","JFK","SFO","ATL","SFO"}.
Another possible reconstruction is {“JFK”,“SFO”,“ATL”,“JFK”,“ATL”,“SFO”}. But it is larger in lexical order.
Note there may be more than one same tickets. For example:
{{'ANU', 'EZE'}, {'ANU', 'JFK'}, {'ANU', 'TIA'}, {'AXA', 'TIA'},
{'EZE', 'AXA'}, {'JFK', 'ANU'}, {'JFK', 'TIA'}, {'TIA', 'ANU'},
{'TIA', 'ANU'}, {'TIA', 'JFK'}}
3.8.9.10. Alien Dictionary
There is a new alien language that uses the lower-case English alphabet. However, the order among the letters is unknown to you.
You are given a list of strings words from the alien language's dictionary, where the strings in words are sorted lexicographically by the rules of this new language.
Return a string of the unique letters in the new alien language sorted in lexicographically increasing order by the new language's rules. If there is no solution, return "". If there are multiple solutions, return any of them.
A string s is lexicographically smaller than a string t if at the first letter where they differ, the letter in s comes before the letter in t in the alien language. If the first min(s.length, t.length) letters are the same, then s is smaller if and only if s.length < t.length.
Example 1:
Input: words = {"wrt","wrf","er","ett","rftt"}
Output: "wertf"
Example 2:
Input: words = {"z","x"}
Output: "zx"
Example 3:
Input: words = {"z","x","z"}
Output: ""
Explanation: The order is invalid, so return "".
3.8.9.11. Is Graph Bipartite?
Given a graph, return true if and only if it is bipartite.
Recall that a graph is bipartite if we can split it’s set of nodes into two independent subsets A and B such that every edge in the graph has one node in A and another node in B.
The graph is given in the following form: graph[i] is a list of indexes j for which the edge between nodes i and j exists. Each node is an integer between 0 and graph.length - 1. There are no self edges or parallel edges: graph[i] does not contain i, and it doesn’t contain any element twice. The graph may not be connected.
Example 1:
Input: {{1,3}, {0,2}, {1,3}, {0,2}}
Output: true
Explanation:
The graph looks like this:
0----1
| |
| |
3----2
We can divide the vertices into two groups: {0, 2} and {1, 3}.
Example 2:
Input: {{1,2,3}, {0,2}, {0,1,3}, {0,2}}
Output: false
Explanation:
The graph looks like this:
0----1
| \ |
| \ |
3----2
We cannot find a way to divide the set of nodes into two independent ubsets.
The graph is given in adjacency list form with the vector index as the key. We can use another extra color vector to track the color of visited nodes, while it is also used as visited set to check if a node has been visited.
BFS
color: 0 ==> unknown, 1 ==> black, -1 ==> red
1bool isBipartite_BFS(vector<vector<int>> &graph) {
2 int N = graph.size(), t;
3 vector<int> color(N);
4 for (int k = 0; k < N; k++) {
5 if (color[k] != 0) continue;
6 color[k] = 1;
7 queue<int> q;
8 q.push(k);
9 while (!q.empty()) {
10 t = q.front(), q.pop();
11 for (int neighbour : graph[t]) {
12 if (color[neighbour] == 0) {
13 color[neighbour] = color[t] * -1;
14 q.push(neighbour);
15 } else if (color[neighbour] == color[t])
16 return false;
17 }
18 }
19 }
20 return true;
21}
DFS
color: -1 ==> unknown, 0 ==> black, 1 ==> red
1bool isBipartite_DFS(vector<vector<int>> &graph) {
2 int N = graph.size(), t;
3 vector<int> color(N, -1);
4 for (int k = 0; k < N; k++) {
5 if (color[k] > 0) continue;
6 color[k] = 0;
7 stack<int> stk;
8 stk.push(k);
9 while (!stk.empty()) {
10 t = stk.top(), stk.pop();
11 for (int i : graph[t]) {
12 if (color[i] == -1) {
13 color[i] = color[t] ^ 1, stk.push(i);
14 } else if (color[i] == color[t])
15 return false;
16 }
17 }
18 }
19 return true;
20}
🐾 To generate alternate sequence, we can do 1*-1*-1... or 0^1^1^1....
3.8.9.12. Cheapest Flights Within K Stops
There are n cities connected by m flights. Each fight starts from city u and arrives at v with a price w.
Now given all the cities and fights, together with starting city src and the destination dst, your task is to find the cheapest price from src to dst with up to k stops. If there is no such route, output -1.
Example:
+---+
| 0 |
+---+
/ \
100 500
/ \
v v
+---+ +---+
| 1 | ---100---> | 2 |
+---+ +---+
Input: n = 3, edges = {{0,1,100},{1,2,100},{0,2,500}}, src = 0, dst = 2, k = 1; Output: 200
The cheapest price from city 0 to city 2 with at most 1 stop costs 200(0->1->2).
Input: n = 3, edges = {{0,1,100},{1,2,100},{0,2,500}}, src = 0, dst = 2, k = 0; Output: 500
The cheapest price from city 0 to city 2 with at most 0 stop costs 500(0->2).
Brute Force (DFS)
1struct Solution_Brute_Force_DFS {
2 int mi = INT_MAX, dst, src, K;
3 unordered_map<int, unordered_map<int, int>> g;
4 int best_price(int n, const vector<vector<int>>& flights, int _src, int _dst, int k) {
5 g.clear();
6 for (int i = 0; i < flights.size(); i++)
7 g[flights[i][0]][flights[i][1]] = flights[i][2];
8 src = _src, dst = _dst, K = k + 1;
9 dfs(0, 0, src);
10 return mi == INT_MAX ? -1 : mi;
11 }
12 void dfs(int x, int p, int c) {
13 if (mi <= p) return;
14 if (dst == c) {
15 mi = min(mi, p);
16 return;
17 }
18 if (K == x) return;
19 for (const auto &[d, price] : g[c])
20 dfs(x + 1, p + price, d);
21 }
22};
We can use Memoization to optimize the DFS algorithm.
Bellman Ford
An important part to understanding the Bellman Ford’s working is that at each step, the relaxations lead to the discovery of new shortest paths to nodes. After the first iteration over all the vertices, the algorithm finds out all the shortest paths from the source to nodes which can be reached with one hop (one edge). That makes sense because the only edges we’ll be able to relax are the ones that are directly connected to the source as all the other nodes have shortest distances set to inf initially.
Similarly, after the (K+1)th step, Bellman-Ford will find the shortest distances for all the nodes that can be reached from the source using a maximum of K stops. Isn’t that what the question asks us to do? If we run Bellman-Ford for K+1 iterations, it will find out shortest paths of length K or less and it will find all such paths. We can then check if our destination node was reached or not and if it was, then the value for that node would be our shortest path!
1int best_price(int n, const VVI &flights, int src, int dst, int k) {
2 unordered_map<int, unordered_map<int, int>> graph;
3 for (auto &e : flights) graph[e[0]][e[1]] = e[2];
4 unordered_map<int, int> costs = graph[src];
5 while (k--) { // O(k)
6 auto tmp = costs;
7 for (const auto& [nd, cost] : tmp) {
8 unordered_map<int, int> &next = graph[nd];
9 for (const auto& [next_node, weight] : next) // O(V)
10 if (costs.count(next_node)) {
11 costs[next_node] = min(costs[next_node], cost + weight);
12 } else
13 costs[next_node] = cost + weight;
14 }
15 }
16 return costs.count(dst) ? costs[dst] : -1;
17}
Line 6: To modify the unordered_map when looping through it, we need to make a copy first and then loop the copy.
Dijkstra
As for Dijkstra, here we can’t do relaxation, because if the smaller cost path has more than k stops it won’t be valid!
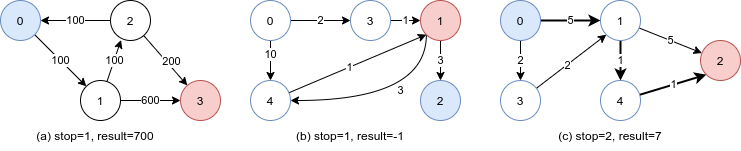
Figure 3.8.7 Test cases for cheapest flights
In Figure 3.8.7, case a and c will have result 400 and 6 respectively if there is no constraint of most k stops.
1int best_price_v2(int n, const VVI &flights, int src, int dst, int k) {
2#define TI3 tuple<int,int,int>
3 unordered_map<int, unordered_map<int, int>> g;
4 vector<int> dist(n + 1, INT_MAX), stops(n+1, INT_MAX);
5 for(auto& v: flights) g[v[0]][v[1]] = v[2];
6 priority_queue<TI3, vector<TI3>, greater<>> q;
7 q.emplace(0, src, 0);
8 while(!q.empty()){
9 const auto [cost, node, step] = q.top(); q.pop();
10 if (node==dst) return cost;
11 if (step>k or step>=stops[node]) continue;
12 for(auto& nei: g[node])
13 stops[node]=step, q.emplace(cost + g[node][nei.first], nei.first, step+1);
14 }
15 return -1;
16}
Reference: Section 3.8.6.2, Section 3.8.6.1
3.8.9.13. Lowest Price With Shopping Offers
In a store, there are some kinds of items to sell. Each item has a price.
However, there are some special offers, and a special offer consists of one or more different kinds of items with a sale price.
You are given the each item’s price, a set of special offers, and the number we need to buy for each item. The job is to output the lowest price you have to pay for exactly certain items as given, where you could make optimal use of the special offers.
Each special offer is represented in the form of an array, the last number represents the price you need to pay for this special offer, other numbers represents how many specific items you could get if you buy this offer.
You could use any of special offers as many times as you want.
Example 1:
Input: {2,5}, {{3,0,5},{1,2,10}}, {3,2}
Output: 14
Explanation:
There are two kinds of items, A and B. Their prices are $2 and $5 respectively.
In special offer 1, you can pay $5 for 3A and 0B
In special offer 2, you can pay $10 for 1A and 2B.
You need to buy 3A and 2B, so you may pay $10 for 1A and 2B (special offer #2), and $4 for 2A.
Example 2:
Input: {2,3,4}, {{1,1,0,4},{2,2,1,9}}, {1,2,1}
Output: 11
Explanation:
The price of A is $2, and $3 for B, $4 for C.
You may pay $4 for 1A and 1B, and $9 for 2A ,2B and 1C.
You need to buy 1A ,2B and 1C, so you may pay $4 for 1A and 1B (special offer #1), and $3 for 1B, $4 for 1C.
You cannot add more items, though only $9 for 2A ,2B and 1C.
Note: There are at most 6 kinds of items, 100 special offers.
For each item, you need to buy at most 6 of them.
You are not allowed to buy more items than you want, even if that would lower the overall price.
3.8.9.14. Valid Path With Landmark
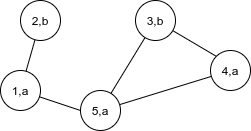
N cities from 1 to N, each city has either landmark A or B.
Return true if there is a path from x to y so that path has the specified landmark, otherwise return false
Example:
Landmarks: 1:a,2:b,3:b,4:a,5:a
Paths: 1-2, 1-5, 3-4, 3-5, 4-5
input: (1, 4, a); output: true
from 1 to 4, there are two paths: 1=>5=>4 is not valid because there is no landmark b in the path. However, there is another pat 1=>5=>3=>4, which has b in it, so return true.
To return true, there are two conditions: path exists, and the path contains at least one specific landmark.
1unordered_map<int, char> c2lm;
2unordered_map<int, unordered_set<int>> graph;
3void build_graph() {
4 c2lm = {{1, 'a'}, {2, 'b'}, {3, 'b'}, {4, 'a'}, {5, 'a'}};
5 graph = {{1, {2, 5}}, {2, {1}}, {3, {4, 5}}, {4, {3, 5}}, {5, {4, 3, 1}}};
6}
7void build_graph_v2() {
8 build_graph();
9 c2lm = {{1, 'a'}, {2, 'a'}, {3, 'b'}, {4, 'a'}, {5, 'a'}};
10}
11
12// return if we can reach tar from src and has_lm is true
13bool dfs(int src, int tar, bool has_lm, char lmk, unordered_set<int>& vd) {
14 if (!has_lm and c2lm[src] == lmk) has_lm = true;
15 if (src == tar) return has_lm;
16 for (int city : graph[src]) {
17 if (vd.count(city)) continue;
18 vd.insert(city);
19 if (dfs(city, tar, has_lm, lmk, vd)) return true;
20 vd.erase(city);
21 }
22 return false;
23}
24
25bool valid_path_with_landmark(int src, int tar, char lmk) {
26 unordered_set<int> vd;
27 vd.insert(src);
28 return dfs(src, tar, false, lmk, vd);
29}
3.8.9.15. Minimum Height Trees
For a undirected graph with tree characteristics, we can choose any node as the root. The result graph is then a rooted tree. Among all possible rooted trees, those with minimum height are called minimum height trees (MHTs). Given such a graph, write a function to find all the MHTs and return a list of their root labels.
Format:
The graph contains n nodes which are labeled from 0 to n - 1. You will be given the number n and a list of undirected edges (each edge is a pair of labels).
You can assume that no duplicate edges will appear in edges. Since all edges are undirected, {0, 1} is the same as {1, 0} and thus will not appear together in edges.
Example 1: Given n = 4, edges = {{1, 0}, {1, 2}, {1, 3}}, return {1}.
0
|
1
/ \
2 3
Example 2: Given n = 6, edges = {{0, 3}, {1, 3}, {2, 3}, {4, 3}, {5, 4}}, return {3, 4}.
0 1 2
\ | /
3
|
4
|
5
This question is about an undirected graph. And it is also a tree, so there is no circle! So using Khan Algo’s idea is like to peel an onion! But when will it be peeled? Because there is no circle, so to It ends when there are only 2 or 1 node left. How to determine the outermost leaf node? We should check if degree(undirected graph) or in-degree(DAG) is one.
1vector<int> findMinHeightTrees(int n, vector<pair<int, int>>& edg) {
2 if (n == 1) return {0}; // edge case of one node
3 map<int, set<int>> g;
4 for (auto& pr : edg)
5 g[pr.first].insert(pr.second), g[pr.second].insert(pr.first);
6 while (g.size() > 2) {
7 set<int> leaves;
8 auto it = g.begin();
9 while (it != g.end())
10 if (it->second.size() == 1)
11 leaves.insert(it->first), it = g.erase(it);
12 else
13 it++;
14 if (g.size() <= 2) break;
15 for (auto& pr : g) { // remove connection with leaves from peer side
16 auto itr = pr.second.begin();
17 while (itr != pr.second.end())
18 if (leaves.count(*itr))
19 itr = pr.second.erase(itr);
20 else
21 itr++;
22 }
23 }
24 vector<int> r;
25 for (auto& pr : g) r.push_back(pr.first);
26 return r;
27}
The implementation of this solution involves how to delete elements from the STL container in a loop, one of the bug-prone areas.
3.8.9.16. Reconstruct Graph With Parent Nodes When Peeling Nodes
Given an undirected tree, also a graph, delete a leaf node on the graph each time, and put the adjacent node(s) connected to the leaf node into an array, until there are only two nodes in the graph. When there are multiple leaves to delete, start from the minimum numbered node. The problem is that given this array, reconstruct the structure of the graph.
Function signature is: vector<pair<int,int>> reconstruct_tree(int n, vector<int>);
N = 7 mean a tree with 7 nodes tagged from 1 to 7. The node removal algorithm goes as follows:
1. original tree
1-----5-----6------7-----4 {}
| |
2 3
2. delete 1 and add 5
5-----6------7-----4 {5}
| |
2 3
3. delete 2 and add 5
5-----6------7-----4 {5,5}
|
3
4. delete 3 and add 6
5-----6------7-----4 {5,5,6}
5. delete 4 and add 7
5-----6------7 {5,5,6,7}
6. delete 5 and add 6
6------7 {5,5,6,7,6}
7. stop
The calling reconstruct_tree(7, {5,5,6,7,6}) should reconstruct the original tree.
Another example: calling reconstruct_tree(4, {2,2}) will reconstruct the following tree {{2,1},{3,2},{4,2}}:
1
|
2
/ \
3 4
The elements in the input list start out as parents, and at some point they become leaves.
Two steps: 1. Find the initial leaf node (the outermost leaf) and connect the outermost leaf to their parent. 2. The key is how to find the inner leaf node. You can use a counter to count the elements in the input list. Each time an element is connected to a leaf, the counter is reduced by 1. When the counter is 0, it means that the parent has become a new leaf, add it to leaf sets. Until I have seen all the elements in the input list, there are still two points in the leaf sets, which are the two innermost nodes.
1vector<pair<int, int>> reconstruct_tree(int n, vector<int> v) {
2 map<int, int> counter;
3 list<int> leaves;
4 vector<pair<int, int>> res;
5 for (int i : v) counter[i]++;
6 for (int i = 1; i <= n; i++)
7 if (!counter.count(i)) leaves.push_back(i);
8 auto add_ = [&res](int x, int y) {
9 if (x < y) swap(x, y);
10 res.emplace_back(x, y);
11 };
12 while (!leaves.empty()) {
13 auto it = leaves.begin();
14 leaves.pop_front();
15 int v0 = v[0];
16 v.erase(v.begin());
17 add_(*it, v0);
18 if (--counter[v0] == 0) {
19 leaves.push_back(v0);
20 counter.erase(v0);
21 if (counter.empty()) {
22 break;
23 }
24 }
25 }
26 add_(leaves.front(), leaves.back());
27 return res;
28}
3.8.9.17. Shortest Path in a Grid with Obstacles Elimination
You are given an m x n integer matrix grid where each cell is either 0 (empty) or 1 (obstacle). You can move up, down, left, or right from and to an empty cell in one step.
Return the minimum number of steps to walk from the upper left corner (0, 0) to the lower right corner (m - 1, n - 1) given that you can eliminate at most k obstacles. If it is not possible to find such walk return -1.
Example 1:
j---> > >
0 1 2
+---+---+---+
i 0 | | | |
| +---+---+---+
v 1 | x | x | x |
v +---+---+---+
v 2 | | x | |
+---+---+---+
Input: grid = {{0,0,0},{1,1,1},{0,1,0}}, k = 1
Output: 4
Explanation:
The shortest path is (0,0) -> (0,1) -> (0,2) -> (1,2) -> (2,2).
Example 2:
j---> > >
0 1 2
+---+---+---+
i 0 | | | x |
| +---+---+---+
v 1 | x | x | x |
v +---+---+---+
v 2 | x | x | |
+---+---+---+
Input: grid = {{0,0,1},{1,1,1},{1,1,0}}, k = 1
Output: -1
Explanation: We need to eliminate at least two obstacles to find such a walk.
In regular BFS, each node in the graph is denoted as the position {x, y} in the grid. But in this question, we also want to track how many obstacles we have destroyed so far.
steps obstacles
0 1 2 0 1 2
+---+---+---+ +---+---+---+
0 | 0 | 1 | 2 | 0 | 0 | 0 | 0 |
+---+---+---+ +---+---+---+
1 | 1 | 2 | 3 | 1 | 1 | 1 | 1 |
+---+---+---+ +---+---+---+
2 | 2 | 3 | 4 | 2 | 1 | 2 | 1 |
+---+---+---+ +---+---+---+
steps obstacles
0 1 2 0 1 2
+---+---+---+ +---+---+---+
0 | 0 | 1 | 2 | 0 | 0 | 0 | 1 |
+---+---+---+ +---+---+---+
1 | 1 | 2 | 3 | 1 | 1 | 1 | 2 |
+---+---+---+ +---+---+---+
2 | 2 | 3 | 4 | 2 | 2 | 2 | 2 |
+---+---+---+ +---+---+---+
This question is just two steps more than regular medium BFS question. All we need to do is to add one demension to track the visit path and one more variable(co - count of obstacles) to track how many obstacles we have encountered. Once we get those two things sorted out, we can easily code up the solution with regular “BFS formula”.
1int shortestPath(vector<vector<int>> grid, int k) {
2 if(grid.empty() or grid[0].empty()) return -1;
3 const vector<int> dirs{0, 1, 0, -1, 0};
4 const int M = grid.size(), N = grid[0].size();
5 vector<vector<int>> seen(M, vector<int>(N, INT_MAX));
6 queue<tuple<int, int, int>> q;
7 int steps = 0;
8 q.emplace(0, 0, 0);
9 seen[0][0] = 0;
10 while (!q.empty()) {
11 int sz = q.size();
12 while (sz--) {
13 auto [x, y, co] = q.front(); q.pop();
14 if (x == M - 1 and y == N - 1) return steps;
15 for (int i = 0; i < 4; ++i) {
16 int x2 = x + dirs[i + 1], y2 = y + dirs[i];
17 if (x2 < 0 or y2 < 0 or x2 >= M or y2 >= N) continue;
18 int o2 = co + grid[x2][y2];
19 if (o2 >= seen[x2][y2] or o2 > k) continue;
20 seen[x2][y2] = o2;
21 q.emplace(x2, y2, o2);
22 }
23 }
24 ++steps;
25 }
26 return -1;
27}
3.8.9.18. Wall In Gird World
A 2D array in which 0 is an open space and 1 is a wall. If you can remove at most one wall, can you reach the lower right cell from the upper left cell?
Example:
{0, 0, 0, 1, 0, 0} {-, -, -, 1, 0, 0}
{1, 1, 0, 1, 0, 0} {1, 1, -, 1, 0, 0}
{0, 0, 0, 0, 0, 0} --> {0, 0, -, -, -, -}
{1, 1, 1, 1, 1, 1} {1, 1, 1, 1, 1, -}
{0, 0, 0, 0, 1, 0} {0, 0, 0, 0, 1, -}
The answer is true for the above example and the possible path is marked as `-`.
Follow up: to reach the bottom right cell, at least how many walls you need to remove?
Example:
{0, 1, 0, 1, 0, 1} {-, 1, 0, 1, 0, 1}
{1, 1, 0, 1, 0, 0} {-, 1, 0, 1, 0, 0}
{0, 0, 0, 1, 1, 0} --> {-, 0, 0, 1, 1, 0}
{1, 1, 1, 1, 1, 1} {-, 1, 1, 1, 1, 1}
{0, 0, 0, 0, 1, 0} {-, -, -, -, -, -}
One possible path is marked as `-` above. The walls to remove number is 3.
1int bfs_follow_up(vector<vector<int>> &g) {
2 if (g.empty() or g[0].empty()) return 0;
3 int R = g.size(), C = g[0].size();
4 vector<vector<int>> dist(R, vector<int>(C, R * C + 1));
5 queue<array<int, 2>> q;
6 dist[0][0] = g[0][0];
7 q.push({0, 0});
8 int dir[] = {-1, 0, 1, 0, -1};
9 while (!q.empty()) {
10 auto h = q.front();
11 q.pop();
12 for (int i = 0; i < 4; i++) {
13 int x = h[0] + dir[i], y = h[1] + dir[i + 1];
14 if (x < 0 || x >= R || y < 0 || y >= C || dist[x][y] <= dist[h[0]][h[1]] + g[x][y]) continue;
15 dist[x][y] = dist[h[0]][h[1]] + g[x][y];
16 q.push({x, y});
17 }
18 }
19 for(auto v: dist){for(int x: v) cout << x << " "; cout << endl;}
20 return dist[R - 1][C - 1];
21}
The following is the number-of-walls-removed matrix.
0 1 1 2 2 3
1 2 1 2 2 2
1 1 1 2 3 2
2 2 2 3 4 3
2 2 2 2 3 3
3.8.9.19. 8-Puzzle
The 8-puzzle problem is a puzzle invented and popularized by Noyes Palmer Chapman in the 1870s. It is played on a 3-by-3 grid with 8 square blocks labeled 1 through 8 and a blank square. Your goal is to rearrange the blocks so that they are in order. You are permitted to slide blocks horizontally or vertically into the blank square. The following shows a sequence of legal moves from an initial board position (left) to the goal position (right).
1 3 1 3 1 2 3 1 2 3 1 2 3
4 2 5 => 4 2 5 => 4 5 => 4 5 => 4 5 6
7 8 6 7 8 6 7 8 6 7 8 6 7 8
initial goal
Solution: Best-First Search.
We now describe an algorithmic solution to the problem that illustrates a general artificial intelligence methodology known as the A* Search algorithm. We define a state of the game to be the board position, the number of moves made to reach the board position, and the previous state. First, insert the initial state (the initial board, 0 moves, and a null previous state) into a priority queue. Then, delete from the priority queue the state with the minimum priority, and insert onto the priority queue all neighboring states (those that can be reached in one move). Repeat this procedure until the state dequeued is the goal state. The success of this approach hinges on the choice of priority function for a state. We consider two priority functions:
Hamming priority function. The number of blocks in the wrong position, plus the number of moves made so far to get to the state. Intutively, a state with a small number of blocks in the wrong position is close to the goal state, and we prefer a state that have been reached using a small number of moves. Manhattan priority function. The sum of the distances (sum of the vertical and horizontal distance) from the blocks to their goal positions, plus the number of moves made so far to get to the state. For example, the Hamming and Manhattan priorities of the initial state below are 5 and 10, respectively.
8 1 3 1 2 3 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8
4 2 4 5 6 ---------------------- ----------------------
7 6 5 7 8 1 1 0 0 1 1 0 1 1 2 0 0 2 2 0 3
initial goal Hamming = 5 + 0 Manhattan = 10 + 0
We make a key oberservation: to solve the puzzle from a given state on the priority queue, the total number of moves we need to make (including those already made) is at least its priority, using either the Hamming or Manhattan priority function. (For Hamming priority, this is true because each block that is out of place must move at least once to reach its goal position. For Manhattan priority, this is true because each block must move its Manhattan distance from its goal position. Note that we do not count the blank tile when computing the Hamming or Manhattan priorities.)
Consequently, as soon as we dequeue a state, we have not only discovered a sequence of moves from the initial board to the board associated with the state, but one that makes the fewest number of moves. (Challenge for the mathematically inclined: prove this fact.)
1int solve_8puzzle_bfs(TMatrix a) {
2 priority_queue<state, vector<state>, cmp> q; // min heap
3 q.push(state(a, 0));
4 while (!q.empty()) {
5 auto t = q.top();
6 q.pop();
7 TMatrix& c = t.first;
8 int moves_so_far = t.second;
9 visited.insert(c);
10 if (c == GOAL) {
11 return moves_so_far;
12 }
13 for (const auto &ch: get_children(c)) {
14 if (visited.count(ch)==0) {
15 parent[ch] = c;
16 q.emplace(ch, moves_so_far + 1);
17 }
18 }
19 }
20 return 0;
21}
1// {matrix, steps_so_far}
2using state = pair<TMatrix, int>;
3const TMatrix GOAL = {{1, 2, 3},
4 {4, 5, 6},
5 {7, 8, 0}};
6// moves - from original matrix, to the current matrix, how many steps we have
7// or moved after `moves` steps, the original matrix becomes the current matrix
8int manhattan_to_goal(const TMatrix ¤t_matrix, int moves) {
9 int distance = moves;
10 for (int i = 0; i < 3; i++) {
11 for (int j = 0; j < 3; j++) {
12 if (current_matrix[i][j] != 0) {
13 int t = current_matrix[i][j];
14 for (int k = 0; k < 3; k++) {
15 for (int l = 0; l < 3; l++) {
16 if (t == GOAL[k][l])
17 distance += abs(i - k) + abs(j - l); // manhattan distance
18 }
19 }
20 }
21 }
22 }
23 return distance;
24}
25
26struct cmp { // min heap
27bool operator()(const state &a, const state &b) {
28 return manhattan_to_goal(a.first, a.second) > manhattan_to_goal(b.first, b.second);
29}
30};
3.8.9.20. Magic Squares
After inventing the globally popular Rubik’s Cube, Mr. Rubik came up with its 2D version called the Rubik’s Board. It consists of 8 equally-sized squares arranged as follows:
1 2 3 4
8 7 6 5
Each square of the Rubik’s Board is colored. These 8 colors are represented by the first 8 positive integers. A sequence of colors can represent a state of the Rubik’s Board. Starting from the top-left square and going clockwise, we form a color sequence. For example, the state depicted above is represented by the sequence 1,2,3,4,5,6,7,8. This is the basic state.
Three basic operations are provided, denoted by uppercase letters A, B, and C (these operations can alter the state of the Rubik’s Board):
A: Swap the top and bottom rows.
B: Move the rightmost column to the leftmost position.
C: Rotate the middle part of the board clockwise.
Here are demonstrations of these operations on the basic state:
A:
8 7 6 5
1 2 3 4
B:
4 1 2 3
5 8 7 6
C:
1 7 2 4
8 6 3 5
For each possible state, these three basic operations can be used.
Your task is to program and compute the minimum number of basic operations required to transform the basic state into a specific state, and output the sequence of basic operations.
Example Input:
2 6 8 4 5 7 3 1
Example Output:
7, BCABCCB
We can use BFS to solve this question.
1 set<TMatrix> visited;
2 TMatrix TARGET = {{2, 6, 8, 4},
3 {1, 3, 7, 5}};
4 pair<int, string> magic_squares_bfs(const TMatrix &m) {
5 queue<pair<TMatrix, string>> q;
6 q.emplace(m, "");
7 visited.insert(m);
8 while (not q.empty()) {
9 auto e = q.front();
10 q.pop();
11 if (e.first == TARGET)
12 return {e.second.size(), e.second};
13 auto a = get_A(e.first);
14 auto b = get_B(e.first);
15 auto c = get_C(e.first);
16 if (!visited.count(a)) q.emplace(a, e.second + "A"), visited.insert(a);
17 if (!visited.count(b)) q.emplace(b, e.second + "B"), visited.insert(b);
18 if (!visited.count(c)) q.emplace(c, e.second + "C"), visited.insert(c);
19 }
20 return {0, ""};
21 }
3.8.9.21. Sort Matrix By Swap
Given an NxN matrix with unique integer, find the sequence of swap to get a sorted matrix.
Example:
+---+---+---+ +---+---+---+
| 1 | 3 | 2 | | 1 | 2 | 3 |
+---+---+---+ +---+---+---+
| 4 | 5 | 9 | => | 4 | 5 | 6 |
+---+---+---+ +---+---+---+
| 7 | 8 | 6 | | 2 | 8 | 9 |
+---+---+---+ +---+---+---+
The output is: [[2,3],[6,9]]
The solution is obviously A*.
3.8.9.22. Robot Car
A robot car starts at position 0 and speed +1 on an infinite number line. The car can go into negative positions. it car drives automatically according to a sequence of instructions 'A' (accelerate) and 'R' (reverse):
When you get an instruction 'A', your car does the following:
position += speed
speed *= 2
When you get an instruction 'R', your car does the following:
If your speed is positive then speed = -1
otherwise speed = 1
Your position stays the same.
For example, after commands "AAR", your car goes to positions 0 --> 1 --> 3 --> 3, and your speed goes to 1 --> 2 --> 4 --> -1.
Given a target position target, return the length of the shortest sequence of instructions to get there.
Example 1:
Input: target = 3, Output: 2
Explanation: The shortest instruction sequence is "AA". Your position goes from 0 --> 1 --> 3.
Example 2:
Input: target = 6, Output: 5
Explanation: The shortest instruction sequence is "AAARA". Your position goes from 0 --> 1 --> 3 --> 7 --> 7 --> 6.
Since this is a shortest path question and we have only two choices A and R, we can use BFS.
0
/ \
1 0
/ \
3 1
/ \
7 3
/ \
15 7
/ \
6 7
1int car(int target) {
2 queue<pair<int, long>> q;
3 q.push({0, 1});
4 int level = 0;
5 while (!q.empty()) {
6 int sz = q.size();
7 for (int i = 0; i < sz; i++) {
8 pair<int, long> t = q.front();
9 q.pop();
10 if (t.first == target) return level;
11 q.push({t.first + t.second, t.second * 2});
12 long sign = t.second < 0 ? 1 : -1;
13 if ((t.first + t.second > target && t.second > 0) or (t.first + t.second < target && t.second < 0))
14 q.emplace(t.first, sign);
15 }
16 level++;
17 }
18 return -1;
19}
20
21} // namespace ns_graph_bfs
22
23using namespace ns_graph_bfs;
3.8.9.23. Expression Add Operators
Given a string that contains only digits 0-9 and a target value, return all possibilities to add binary operators (not unary) +, -, or * between the digits so they evaluate to the target value.
Examples:
"123", 6 -> ["1+2+3", "1*2*3"]
"232", 8 -> ["2*3+2", "2+3*2"]
"105", 5 -> ["1*0+5","10-5"]
"00", 0 -> ["0+0", "0-0", "0*0"]
"3456237490", 9191 -> []
3.8.9.24. Flight Route With Max Fun
There are n cities connected by some number of bi-directional flights and every city has a `fun value` measuring how fun this city is for a tourist. The fun values are additive.
Return the maximum sum of fun values of a flight from a city to another city with exact 2 stops. If no such flight exists, return -1.
Example:
1(2)
/ | \
0(5)---|---2(9)---4(4)
| /
3(8)
Input: fun_value = [5,2,9,8,4], flights = [[0,1],[1,2],[2,3],[0,2],[1,3],[2,4]]
Output: 24 (the flight will travel 0->1->2->3, and the total fun value is 5 + 2 + 9 + 8 = 24.)
Let’s check the example above. The max-fun flight route, or the critical path, is 0->1->2->3. How can we get it?
If we have edge between city 1 and city 2, and they both have many neighbors, the critical path must from two max-fun neighbours of 1 and 2 and they should not be the same.
\ /
--1----2--
/ \
\ /
--1-----2--
\ /
3
1's neighbors: 2(9), 3(8), 0(5)
2's neighbors: 3(8), 0(5), 4(4), 1(2)
it0 end0
1's neighbors: 2(9), 3(8), 0(5)
it1 end1
2's neighbors: 3(8), 0(5), 4(4), 1(2)
We can see the critical path could be 0->1->2->3 or 3->1->2->0.
1#include <gtest/gtest.h>
2#include <sein.hpp>
3
4namespace ns_graph_fun{
5int max_fun(vector<int>& values, vector<vector<int>>& flights) {
6 unordered_map<int, set<pair<int, int>>> m; // insert time is still O(1) because edge size is bounded to 3
7 for (vector<int> &e : flights) {
8 m[e[0]].emplace(values[e[1]], e[1]);
9 if (m[e[0]].size() == 4) m[e[0]].erase(m[e[0]].begin());
10 m[e[1]].emplace(values[e[0]], e[0]);
11 if (m[e[1]].size() == 4) m[e[1]].erase(m[e[1]].begin());
12 }
13 int res = -1;
14 for (vector<int> &e : flights) {
15 auto it0 = m[e[0]].rbegin(), end0 = m[e[0]].rend();
16 auto it1 = m[e[1]].rbegin(), end1 = m[e[1]].rend();
17 if (it0->second == e[1]) it0++;
18 if (it1->second == e[0]) it1++;
19 while (it0->second == it1->second) {
20 auto nextIt0 = next(it0);
21 auto nextIt1 = next(it1);
22 while (nextIt0 != end0 && nextIt0->second == e[1]) nextIt0++;
23 while (nextIt1 != end1 && nextIt1->second == e[0]) nextIt1++;
24 if (nextIt0 == end0 && nextIt1 == end1) {
25 it0 = end0, it1 = end1;
26 break;
27 }
28 if (nextIt0 == end0) {
29 it1 = nextIt1;
30 } else if (nextIt1 == end1) {
31 it0 = nextIt0;
32 } else {
33 if (nextIt0->first > nextIt1->first) {
34 it0 = nextIt0;
35 } else {
36 it1 = nextIt1;
37 }
38 }
39 }
40 if (it0 != end0 && it1 != end1) {
41 res = max(res, values[e[0]] + values[e[1]] + it0->first + it1->first);
42 }
43 }
44 return res;
45}
46}
47using namespace ns_graph_fun;
48TEST(_graph_fun, a) {
49 vector<int> values = {5,2,9,8,4};
50 vector<vector<int>> flights = {{0,1},{1,2},{2,3},{0,2},{1,3},{2,4}};
51 EXPECT_TRUE(max_fun(values, flights) == 24);
52}
3.8.9.25. Create Recipes
You have information about n different recipes. You are given a string array recipes and a 2D string array ingredients. The ith recipe has the name recipes[i], and you can create it if you have all the needed ingredients from ingredients[i]. Ingredients to a recipe may need to be created from other recipes, i.e., ingredients[i] may contain a string that is in recipes.
You are also given a string array supplies containing all the ingredients that you initially have, and you have an infinite supply of all of them.
Return a list of all the recipes that you can create. You may return the answer in any order.
Note that two recipes may contain each other in their ingredients.
Example:
Input: recipes = ["bread","sandwich"], ingredients = [["yeast","flour"],["bread","meat"]], supplies = ["yeast","flour","meat"]
Output: ["bread","sandwich"]
Explanation: We can create "bread" since we have the ingredients "yeast" and "flour". We can create "sandwich" since we have the ingredient "meat" and can create the ingredient "bread".
This is a topological sort with BFS question.
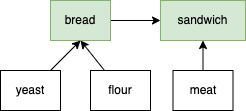
Figure 3.8.8 Graph of Recipes and Ingredients
We use Kahn’s algorithm:
bread(2)----> sandwich(2). bread(0)----> sandwich(1) sandwich(0)
^ ^ ^
/ \ \
yeast(0) flour(0) meat(0)
1namespace ns_topo_recipes{
2vector<string> findAllRecipes(vector<string> recipes, vector<vector<string>> ingredients, vector<string> supplies) {
3 unordered_map<string, unordered_set<string>> g;
4 unordered_map<string, int> indegree;
5 unordered_set<string> rset(recipes.begin(), recipes.end());
6 for(auto& food : supplies) indegree[food] = 0;
7 for(int i = 0; i < recipes.size(); ++i)
8 for(auto& j : ingredients[i])
9 g[j].insert(recipes[i]), indegree[recipes[i]]++;
10 queue<string> q;
11 for(auto& p : indegree){
12 if(p.second == 0)
13 q.push(p.first);
14 }
15 vector<string> ans;
16 while(not q.empty()){
17 string food = q.front(); q.pop();
18 if(rset.find(food) != rset.end())
19 ans.push_back(food);
20 for(auto& nt : g[food]){
21 if(--indegree[nt] == 0)
22 q.push(nt);
23 }
24 }
25 return ans;
26}
27}
28using namespace ns_topo_recipes;
29TEST(_topo_recipes, a) {
30 vector<string> r = findAllRecipes({"bread"},{{"yeast","flour"}},{"yeast","flour","corn"});
31 vector<string> expected = {"bread"};
32 EXPECT_EQ(r, expected);
33}
3.8.9.26. Network Delay Time
You are given a network of n nodes, labeled from 1 to n. You are also given times, a list of travel times as directed edges times[i] = (ui, vi, wi), where ui is the source node, vi is the target node, and wi is the time it takes for a signal to travel from source to target.
We will send a signal from a given node k. Return the minimum time it takes for all the n nodes to receive the signal. If it is impossible for all the n nodes to receive the signal, return -1.
Example 1:
(2)--1--> (1)
\
\--1--> (3) --1--> (4)
Input: times = [[2,1,1],[2,3,1],[3,4,1]], n = 4, k = 2
Output: 2
Example 2:
Input: times = [[1,2,1]], n = 2, k = 1
Output: 1
Example 3:
Input: times = [[1,2,1]], n = 2, k = 2
Output: -1
3.8.9.27. City Traveler
Give a 2-d matrix, where each cell represents a city and each city has a traffic light. Initially all the light are red. At the beginning, the number of each cell represents the time when the red light turns green. When it turns to greeen, it means that you can leave the city. Red light indicates that you can't leave the city. You can travel in two directions: down and right.
Return the shortest time you can travel from upper left to lower right city.
Example input:
{{1, 2, 0},
{4, 6, 5},
{9, 6, 5}}
output: 5
Solution: DP
dp[i][j] = Min(dp[i-1][j],dp[i][j-1])
👽 Follow up: travel in four directions: up, down, left, right
{{1, 1, 1},
{K, K, 1},
{6, 6, 5},
{1, K, K},
{1, 1, 1},
{1, K, 5}}
Dijkstra: cost(i1j1, i2j2) = grid[i1][j1]
3.8.9.28. Count Lakes
A satellite image contains pixels tagged by letter ‘x’ and sign ‘.’, where ‘x’ means land and ‘.’ means water. The defition of lake is a water area all surrounded by lands. In the following sample image, for example, (8,a) is not a lake, but (4,c) and (4, d) form a lake.
Sample Image:
a b c d e f g h i j k l m n o p q
0 {., ., ., ., ., ., ., ., ., ., ., ., ., ., ., ., .}
1 {., ., ., ., ., ., ., ., ., ., ., ., ., ., ., ., .}
2 {., ., ., ., ., ., ., ., ., ., ., ., ., ., ., ., .}
3 {., x, x, x, x, x, ., ., x, ., ., ., ., ., x, x, .}
4 {., x, ., ., x, ., ., ., x, ., ., ., x, x, ., x, x}
5 {., x, x, x, x, ., ., ., x, ., x, x, ., x, ., x, .}
6 {., ., ., ., x, ., ., ., ., ., ., x, ., x, x, x, .}
7 {x, x, ., ., x, ., ., ., ., ., ., x, x, x, ., x, .}
8 {., x, ., ., ., ., ., ., ., ., ., ., ., ., ., ., .}
9 {x, x, ., ., ., ., ., ., ., ., ., ., ., ., ., ., .}
Please implement a count_lakes function to count the number of lakes surrounded by lands connected by the input coordinates.
Examples:
count_lakes(image,(3,i)) -> 0
count_lakes(image,(3,f)) -> 1
count_lakes(image,(6,n)) -> 2
count_lakes(image,(7,b)) -> 0
count_lakes(image,(7,j)) -> 0
There are two steps to solve this problem. First, we need to find the smallest sub-matrix which contains the input coordinates. Then we count the lake number by finding cluster of water. We can use DFS or BFS. The sample code uses DFS.
1class Solution {
2 int R, C;
3 int minx=INT_MAX, miny=INT_MAX, maxx=INT_MIN, maxy=INT_MIN;
4public:
5 void dfs1(vector<string> &m, int x, int y){ // find sub-matrix by land
6 m[x][y] = 'v'; // 💣
7 minx=min(x, minx), miny=min(miny, y), maxx=max(x, maxx), maxy=max(y, maxy);
8 for(int i=-1;i<=1;i++)
9 for(int j=-1;j<=1;j++)
10 if(i or j){ // 💣
11 if(x+i<0 or x+i>=R or y+j<0 or y+j>=C) continue;
12 if (m[x+i][y+j]=='x') dfs1(m,x+i,y+j);
13 }
14 }
15 void dfs2(vector<string>& m, int x, int y, bool& is_lake){ // find lake by water
16 m[x][y] = 'z'; // 💣
17 if(x==minx or x==maxx or y==miny or y==maxy) is_lake=false;
18 for(int i=-1;i<=1;i++)
19 for(int j=-1;j<=1;j++)
20 if(abs(x)+abs(y)==1){ // 💣
21 if(x+i<minx or x+i>maxx or y+j<miny or y+j>maxy) continue;
22 if (m[x+i][y+j]=='.') dfs2(m,x+i,y+j, is_lake);
23 }
24 }
25 int count_lakes(vector<string> m, int x, int y) {
26 R = m.size(), C=m[0].size();
27 if(m[x][y]=='.') return 0;
28 dfs1(m, x, y);
29 int res=0;
30 for(int i=minx;i<=maxx;i++)
31 for(int j=miny;j<=maxy;j++)
32 if(m[i][j]=='.'){
33 bool is_lake = true;
34 dfs2(m,i,j, is_lake);
35 is_lake && res++;
36 }
37 return res;
38 }
39};
Note when finding cluster of islands, we use 8 directions, but when finding cluster of water, we use 4 directions. This is because water is connected by up, down, left and right directions, but lands can be connected in a diagonal way. Another trick is mark the cell as a new value when traversing it in order to avoid using a visited set.