3.8.5. Minimum Spanning Tree

A minimum spanning tree of a connected graph is a subset of the edges that forms a tree that includes every vertex, where the sum of the weights of all the edges in the tree is minimized. For a disconnected graph, a minimum spanning forest is composed of a minimum spanning tree for each connected component.

3.8.5.1. A Sample Question

As a network engineer, your task is to establish a network cabling system connecting four villages to provide them with internet access. Each village is assigned an ID from 1 to 4. The distances between the villages are given as follows:

Village 1 to Village 3: 3 units
Village 3 to Village 4: 2 units
Village 4 to Village 2: 10 units
Village 1 to Village 2: 24 units
Village 1 to Village 4: 20 units

Your objective is to determine the minimum total length of cable required to connect all four villages so that every village has internet access. Write a function that computes this minimal total cable length, ensuring that the network spans all villages without any isolations.

 [3]--2--[4]
  |     /   \
  |    /     \
  3   20      10
  |  /         \
  | /           \
 [1]-----24-----[2]

Consider the provided distances as a weighted graph where the villages are nodes, and the cables are edges with weights representing the distances. Your function should implement an algorithm to find the minimum spanning tree of this graph, which corresponds to the optimal configuration of cables with the minimum total length.

3.8.5.2. Prim Algorithm

The algorithm operates by building this tree one vertex at a time, from an arbitrary starting vertex, at each step adding the cheapest possible connection from the tree to another vertex.

Prim algorithm is very similar to dijkstra algorithm and is even simpler.

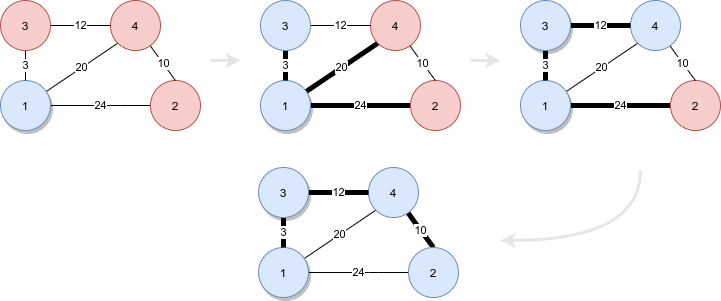
Figure 3.8.2 BFS + Priority Queue ordered by edge weight

int mst_prim(int n, vector<vector<int>> es) {
  unordered_map<int, unordered_map<int, int>> graph;  // node->node->weight
  for (auto &v : es) graph[v[0]][v[1]] = v[2];
  priority_queue<PII, vector<PII>, greater<>> pq;  // min-heap
  vector<int> ds(n + 1, 0);                        // array of weight
  vector<int> parent(n + 1, -1);                   // parent array
  int source = 1;
  pq.emplace(0, source); // {weight, to_node}
  set<int> visited;
  while (!pq.empty()) {
    const auto top = pq.top();
    pq.pop();
    int top_node = top.second;
    if (visited.count(top_node)) continue;
    ds[top_node] = top.first;
    for (const auto &neighbor : graph[top_node]) {  //{node, weight}
      parent[neighbor.first] = top_node;
      pq.emplace(neighbor.second, neighbor.first);
    }
    visited.insert(top_node);
  }
  return accumulate(ds.begin(), ds.end(), 0);
}

Code Block 3.8.1 priority(u) = edge_weight(u)

+---+           +---+           +---+
| s | ========> | u | ------->  | t |
+---+           +---+           +---+

• Prims vs Dijkstra algorithm | MST vs SSSP

3.8.5.3. Kruskal Algorithm

Kruskal’s algorithm finds a minimum spanning forest of an undirected edge-weighted graph. If the graph is connected, it finds a minimum spanning tree. It is a greedy algorithm in graph theory as in each step it adds the next lowest-weight edge that will not form a cycle to the minimum spanning forest.

Figure 3.8.3 Union-Find starting with smallest available edges

int mst_kruskal(int n, const vector<vector<int>> &es) {
  map<int, unordered_map<int, int>> m;  // w => (a -> b), weight-indexed map
  for (auto &v : es) m[v[2]][v[0]] = v[1];
  vector<pair<int, int>> r;
  int sum = 0;
  ch22_union_find::union_find uf(n + 1);
  for (auto &pr : m) {
    auto &mp = pr.second;
    for (auto &ab : mp) {
      if (uf.connected(ab.first, ab.second)) continue;
      r.emplace_back(ab);
      uf.union_(ab.first, ab.second);
      sum += pr.first;
    }
  }
  return sum;
}

The union-find data structure used in line 6 is defined at Section 3.13.2.