3.13.2. Disjoint Set (Union-Find)

The Disjoint Set data structure, also known as Union-Find, is a data structure that tracks a set of elements partitioned into multiple disjoint (non-overlapping) subsets. It’s particularly useful in network connectivity(eg. Section 3.8.5.3), least common ancestors, image processing, and more. The primary operations of this data structure are:

  • Union(x,y): Merge two subsets, represented by x and y, into a single subset.

  • Find(x): Determine which subset a particular element x is in. This can be used for determining if two elements are in the same subset.

3.13.2.1. Optimization Technique

The efficiency of these operations is crucial for many algorithms, and the Union-Find data structure provides a way to perform them efficiently using three optimizations.

  • Path Compression: In a naive Union-Find implementation, the Find operation can become inefficient if the trees become very deep. In the worst case, you might have to traverse a long chain of elements just to find the root. With Path Compression, it flatten the structure of the tree whenever Find() is used, by making every node point directly to the root. This dramatically reduces the time complexity of subsequent find operations.

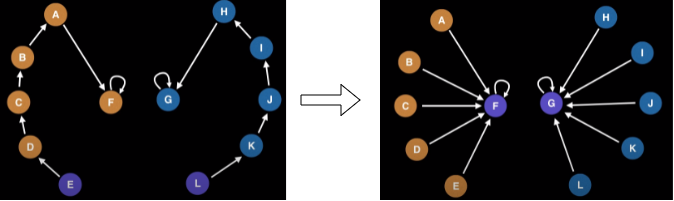
../_images/union_find_path_comp.png

  • Path Havling: Flatten the structure of the tree whenever Find() is used, by making every node point directly to the root. This dramatically reduces the time complexity of subsequent find operations.

  • Union by Size: In Union(), attach the root of the tree with fewer elements to the root of the tree with more elements to avoid increasing the tree height unnecessarily.

The implementation could be the following:

 1struct union_find {
 2  vector<int> bo, sz;
 3  union_find(int z) {
 4    bo.resize(z), sz.resize(z);
 5    iota(bo.begin(), bo.end(), 0); // πŸ’£
 6    fill(sz.begin(), sz.end(), 1);
 7  }
 8  int find(int i) { // find final big boss' index
 9    int j=i;
10    while (bo[i] != i){
11      bo[i]=bo[bo[i]], i = bo[i]; // path halving
12    }
13    return bo[j]=i; // path compression
14  }
15  bool union_(int x, int y) {
16    int bx = find(x), by = find(y);
17    if (bx == by) return false;
18    if (sz[bx] < sz[by])  // merge by rank, winner takes all
19      bo[bx] = by, sz[by] += sz[bx], sz[bx] = 0;
20    else
21      bo[by] = bx, sz[bx] += sz[by], sz[by] = 0;
22    return true;
23  }
24  // retrieve all the peers of `idx`
25  vector<int> get_set(int idx) {
26    vector<int> r;
27    int bi = find(idx);
28    for (int i = 0; i < bo.size(); i++) {
29      if (find(i) == bi) {
30        r.push_back(i);
31      }
32    }
33    return r;
34  }
35  // number of groups
36  int number_of_groups() {
37    // 1. count when bo[i]==i
38    // int res=0;for(int i=0;i<bo.size();i++) res+=int(bo[i]==i); return res;
39    // 2. count sz>0
40    return count_if(sz.begin(), sz.end(), [](int i) { return i > 0; });
41  }
42  bool connected(int x, int y) { return find(x) == find(y); }
43};

In addition to Union(x,y) and Find(x), there are three more functions: get_set(x), number_of_groups(), and connected().

Related Questions:
Reference:

Song:

Title: Union Find
Lyrics: Henry Fuheng Wu

(Verse 1)
Disjoint Set
a.k.a Union-Find
It helps us track sets
with all its might.(all its might)
They are just bunch of trees,
For efficiency,
we put them in some arrays(use two arrays)

(Chorus)
wowo
Union-Find, a super star,
Find your boss
No matter who you are.
Mazes and graphs, it conquers them all,
Union-Find answers the programmer's call.

(Verse 2)
As the name implies,
core functions are union and find,
Yes we can,
optimize it with union by size (winner takes all)
In the find method,
compress and halve the path,
It flatten the trees
so code is fast.

(Outro)
wowo
Union-Find, a super star,
Connecting the elements
No matter how far.
Kruskal minimizes spanning tree
You conquers problems and set us free(set us free)