3.13.5. Order Statistic Tree
In computer science, an order statistic tree is a variant of the binary search tree (or more generally, a B-tree) that supports two additional operations beyond insertion, lookup and deletion:
select(i) // find the i'th smallest element stored in the tree
rank(x) // find the rank of element x in the tree, i.e. its index in the sorted list of elements of the tree
Both operations can be performed in O(log n) worst case time when a self-balancing tree is used as the base data structure.
To have oder statistic, we just need to add a cardinality member variable in the node to represent the node number of the tree with the current node as root.
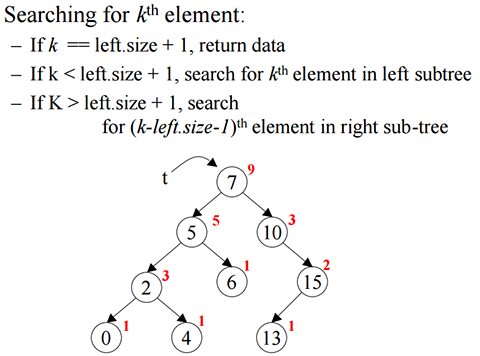
Figure 3.13.2 order statistic tree select algorithm
The node definition could be like Code Block 3.13.1.
1struct node {
2 double val = 0;
3 int card = 1; // 💣 cardinality
4 node *l = nullptr, *r = nullptr;
5 explicit node(double n) : val(n) {}
In GNU STL, we can use GNU Policy-Based STL map as an order statistic tree.
1#include <ext/pb_ds/tree_policy.hpp>
2#include <sein.hpp>
3using namespace __gnu_pbds;
4typedef tree<int, int, less<int>, rb_tree_tag,
5 tree_order_statistics_node_update>
6 ostree;
7
8TEST(_ost, a) {
9 ostree s;
10 s.insert(make_pair(12, 1012));
11 s.insert(make_pair(505, 1505));
12 s.insert(make_pair(30, 1030));
13 s[40] = 123;
14 EXPECT_TRUE(s.find_by_order(0)->second == 1012);
15 EXPECT_TRUE(s.order_of_key(30) == 1);
16}
Related questions: Percentile Query Tree(Section 3.13.8.4)