3.13.1. Bloom Filter
Google’s crawler needs to crawl a large number of web pages every day. So there is a question: whenever a crawler extract a url from a webpage, should it be crawled or not? How to know this url has been crawled? A simple idea is to store the url in a hash table, and look up the table each time to determine whether it exists. If each url occupies 40B, then 1 billion urls will occupy more than 30 GB of memory! Can this be more space efficient?
Can we not store the url itself to greatly reduce the space required? A very classic approach is bitmap. Hash the url, get its index in the bitmap, and check whether the position is 1. This saves space, but it also causes hash collision.
Bloom filter is a probabilistic data structure for the membership query, and it has been intensely experimented in various fields to reduce memory consumption and enhance a system’s performance. The idea of bloom filter is to use multiple independent hash functions to avoid hash collision. A bloom filter is a set-like data structure that is more space-efficient compared to traditional set-like data structures such as hash tables or trees. The catch is a bloom filter can tell you with 100% certainty that something is not in the set, but it can not tell you with 100% certainty that something is in the set.
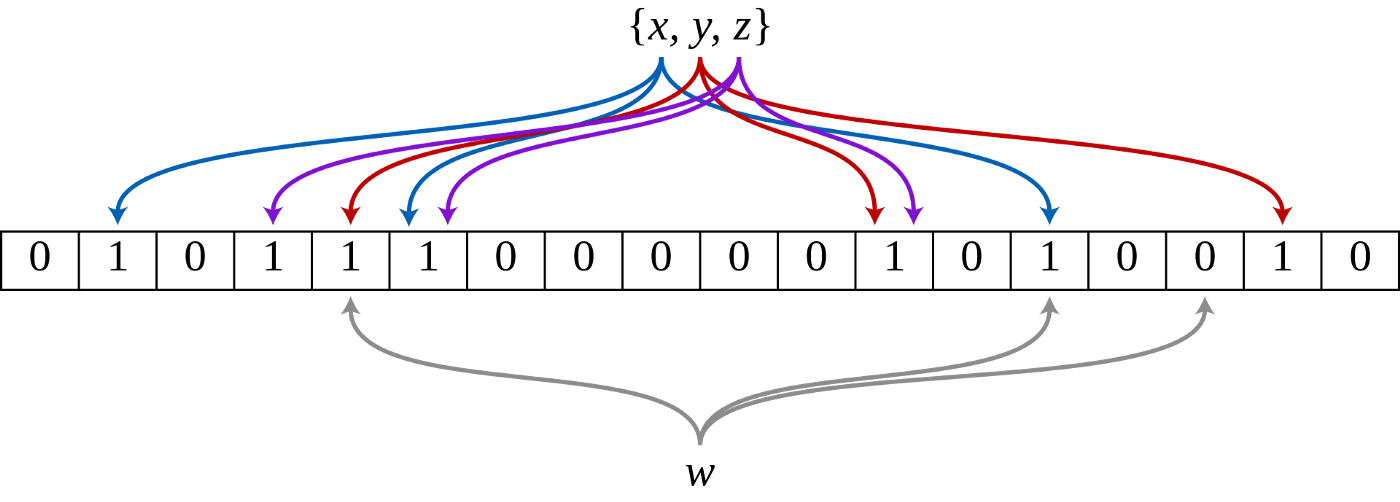
Figure 3.13.1 Bloom Filter: w is not in the set with 100% certainty
3.13.1.1. Standard Bloom Filter
Implement a standard bloom filter. Support the following method:
StandardBloomFilter(k): constructor in which you need to create k hash functions.
add(string): add a string into bloom filter.
contains(string): Check a string whether exists in bloom filter.
Example
1StandardBloomFilter(3)
2add("hello")
3add("code")
4contains("hello") // return true
5contains("world") // return false
The first challeng is how to implement some independent hash functions. The following is an example:
1struct hash_function {
2 int cap, seed;
3 hash_function(int cap_, int seed_): cap(cap_), seed(seed_) {}
4 int hash(string& value) {
5 int ret = 0, n = value.size();
6 for (int i = 0; i < n; ++i) {
7 ret += seed * ret + value[i];
8 ret %= cap;
9 }
10 return ret;
11 }
12};
💡 Here we need to use STL’s bitset. The class template bitset represents a fixed-size sequence of N bits. Bitsets can be manipulated by standard logic operators and converted to and from strings and integers. Method: count, set, reset, test, flip, to_string
1struct standard_bloom_filter {
2 standard_bloom_filter(int k) {
3 while(k--)
4 hash_func.push_back(hash_function(LEN-k, 2*k+3));
5 }
6 void add(string& word) {
7 for (auto h: hash_func)
8 bits.set(h.hash(word));
9 }
10 bool contains(string& word) {
11 for (auto h: hash_func)
12 if (!bits.test(h.hash(word))) return false;
13 return true;
14 }
15 vector<hash_function> hash_func;
16 bitset<LEN> bits; // 💣
17};
3.13.1.2. Counting Bloom Filter
In addition to the problem of false positives, the traditional Bloom Filter has a shortcoming: it cannot support deletion operations. And CBF(Counting Bloom Filter) is used to solve this problem.
Implement a counting bloom filter. Support the following method:
add(string): Add a string into bloom filter.
contains(string): Check a string whether exists in bloom filter.
remove(string): Remove a string from bloom filter.
Example
1CountingBloomFilter(3)
2add("lint")
3add("code")
4contains("lint") // return true
5remove("lint")
6contains("lint") // return false
In CBF, what is maintained is not simply the bits marked 0 or 1, but the counter. For each element in the set, use k hash functions to hash it to obtain k positions, and add 1 to the k counters in the corresponding k positions. When deleting, just decrement the k counters by 1.
So, how many bits should this counter occupy? Allocating too much wastes space; allocating too little is prone to overflow. According to statistic analysis, 4 bits are enough, so we use vector<char> to replace bitset<N> in standard bloom filter.
1struct counting_bloom_filter {
2 // k is number of hash functions
3 counting_bloom_filter(int k) {
4 bits.resize(100000 + k);
5 for (int i = 0; i < k; ++i)
6 hash_func.push_back(hash_function(100000 + i, 2 * i + 3));
7 bits.resize(100000 + k);
8 }
9 void add(string& word) {
10 for (auto& h: hash_func)
11 ++bits[h.hash(word)];
12 }
13 void remove(string& word) {
14 for (auto& h: hash_func)
15 --bits[h.hash(word)];
16 }
17 bool contains(string& word) {
18 for (auto& h: hash_func)
19 if (bits[h.hash(word)] <= 0)
20 return false;
21 return true;
22 }
23 vector<hash_function> hash_func;
24 vector<char> bits; // 💣
25};
One drawback of CBF is the space usage is not very efficient [1].
Footnotes