3.13.4. Interval Tree
The following is an ordered interval tree of non-overlaping intervals. The base data structure is a C++ map(red-black tree).
1struct interval_tree {
2 map<int, int> m;
3 int l = 0;
4 bool overlapped(int a, int b, int x, int y) { return b >= x and a <= y; }
5 void insert(int head, int tail) { // TC: O(N)
6 auto it = m.upper_bound(head); // O(logN)
7 if (it != m.begin()) {
8 it = prev(it);
9 if (overlapped(it->first, it->second, head, tail)) {
10 head = min(it->first, head), tail = max(it->second, tail);
11 l -= (it->second - it->first);
12 it = m.erase(it);
13 }
14 }
15 while (it != m.end()) {
16 if (overlapped(it->first, it->second, head, tail)) {
17 head = min(it->first, head), tail = max(it->second, tail);
18 l -= (it->second - it->first);
19 it = m.erase(it);
20 } else {
21 it++;
22 }
23 }
24 m[head] = tail;
25 l += tail - head;
26 }
27 void remove(int head, int tail){
28 auto it = m.upper_bound(head);
29
30 }
31 bool contains(int x) { // TC: O(LogN)
32 auto it = m.lower_bound(x);
The basic idea is to use map::upper_bound to find the insertion point. Because we use head as the key, we may need to merge the current node with previous node. We also may need to merge all the overlapping nodes after the current node.
The following is a test case for the interval tree.
1TEST(_interval_tree, a) {
2 using namespace ns_interval_tree;
3 auto_profiler ap_("interval_tree");
4 interval_tree itree;
5 vector<pair<int, int>> inputs = {{1, 4}, {5, 6}, {8, 9}, {1, 10}};
6 vector<int> expected = {3, 1, 1, 4};
7 vector<int> r;
8 for (auto &e : inputs) {
9 int prev = itree.l;
10 itree.insert(e.first, e.second);
11 r.push_back(itree.l - prev);
12 }
13 EXPECT_EQ(expected, r);
14}
In the test case, 1-4, 5-6, 8-9 are firstly inserted into the map m. interval_tree_1. Because there is no overlap, no merge operation is required and the insertion is very straightforward.
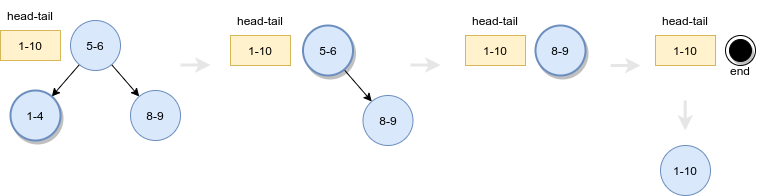
When inserting interval 1-10, there is overlap. A simple algorithm is to use map::upper_bound to find the node which has head greater than 1. The previous node’s head could be equal to 1, so we need to check the previous node. If there is overlap, we delete the node and merge the interval with 1-10. After removing all the overlapped nodes, we insert the merged interval, which is 1-10 in this case. After insertion of 1-10, the tree shrinks to one node.
🐾 Refer to Section 1.4.1 for the usage of map::upper_bound.
👽 How about using lower_bound to solve this problem? 👽 How to find if a value is in the interval tree?