3.8.6. Single-Source Shortest Paths
3.8.6.1. Dijkstra Algorithm
Dijkstra algorithm is used to calculate single source shortest path problem. It can be implemented with BFS and a priority queue.
Take Figure 3.8.4 as an example. To calculate the short path from source node 1 to the other nodes in the graph:
initialize a minium distance table with INT_MAX
put node 1 into a priority queue pq order by distance from node 1
get top node from pq, and skip it if it is in visited set
loop edges of top node, update the minium distance table, and add neighbor node into pq
add top node into visited set, repeat step 2 to 5 until pq is empty

Figure 3.8.4 BFS + Priority Queue ordered by distance to single source
1vector<int> shortest_reach(int n, vector<vector<int>> es, int source) {
2 unordered_map<int, unordered_map<int, int>> edges; // node->node->weight
3 for (auto& v : es) edges[v[0]][v[1]] = v[2];
4 // The PQ is a min-heap to store the `distance from THE source to each node`
5 priority_queue<PII, vector<PII>, greater<>> pq; // min-heap
6 vector<int> ssd(n + 1, INT_MAX); // array of distance to s
7 vector<int> parent(n + 1, -1); // parent array
8 pq.emplace(0, source); // {distance, to_node}
9 set<int> visited;
10 while (!pq.empty()) {
11 const auto top = pq.top();
12 pq.pop();
13 int top_node = top.second;
14 if (visited.count(top_node)) continue;
15 ssd[top_node] = top.first;
16 for (const auto& neighbor : edges[top_node]) { //{node, distance}
17 int d = top.first + edges[top_node][neighbor.first];
18 if (ssd[neighbor.first] > d) { // relax 💣
19 ssd[neighbor.first] = d;
20 parent[neighbor.first] = top_node;
21 pq.emplace(d, neighbor.first);
22 }
23 }
24 visited.insert(top_node);
25 }
26 return ssd;
27}
Dijkstra algorithm greedily chooses which vertex to explore next, according to the value of priority(u) [priority(u) = distance(s,u)] - where distance is the cost so far.
+---+ +---+ +---+
| s | ========> | u | -------> | t |
+---+ +---+ +---+
Dijkstra’s algorithm is a Greedy algorithm and time complexity is O((V+E)LogV) (with the use of Fibonacci heap).
3.8.6.2. Bellman Ford Algorithm
Dijkstra doesn’t work for Graphs with negative weights, Bellman-Ford works for such graphs. Bellman-Ford is also simpler than Dijkstra and suites well for distributed systems. But time complexity of Bellman-Ford is O(VE), which is more than Dijkstra. Code Block 3.8.3 is a sample implementation.
void BellmanFord(struct Graph* graph, int src) {
int V = graph->V, E = graph->E;
// Step 1: Initialize distances from src to all other vertices as INT_MAX
vector<int> dist(V, INT_MAX);
dist[src] = 0;
// Step 2: Relax all edges |V| - 1 times. A simple shortest path from src to any other vertex can have at-most |V| - 1 edges
for (int i = 1; i <= V - 1; i++) {
for (int j = 0; j < E; j++) {
int u = graph->edge[j].src, v = graph->edge[j].dest, weight = graph->edge[j].weight;
if (dist[u] != INT_MAX and dist[u] + weight < dist[v])
dist[v] = dist[u] + weight;
}
}
// Step 3: check for negative-weight cycles. The above step guarantees shortest distances if graph doesn't contain negative weight cycle. If we get a shorter path, there is a cycle.
for (int i = 0; i < E; i++) {
int u = graph->edge[i].src, v = graph->edge[i].dest, weight = graph->edge[i].weight;
if (dist[u] != INT_MAX and dist[u] + weight < dist[v]) {
return; // If negative cycle is detected, simply return
}
}
}
The Kth iteration generates the shortest paths in K steps from src. Section 3.8.9.12 is an example where Bellman Ford is a better fit than Dijkstra.
3.8.6.3. A-Star Algorithm
A-Star is basically an informed variation of Dijkstra. A-Star is considered as a BEST First Search because it greedily chooses which vertex to explore next, according to the value of priority(u) [priority(u) = heuristic(u,t) + distance(s,u)] - where distance is the cost so far.
+---+ +---+ +---+
| s | ========> | u | -------> | t |
+---+ +---+ +---+
A-star could be much faster with the heuristic’s help.
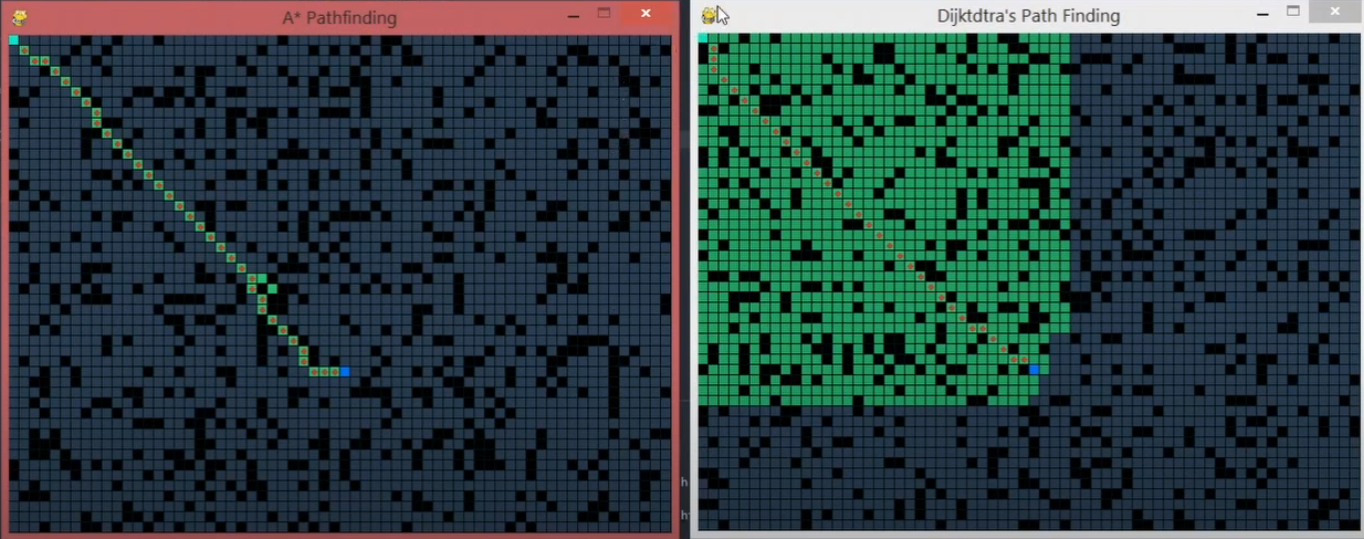
Figure 3.8.5 Path finding without obstacle
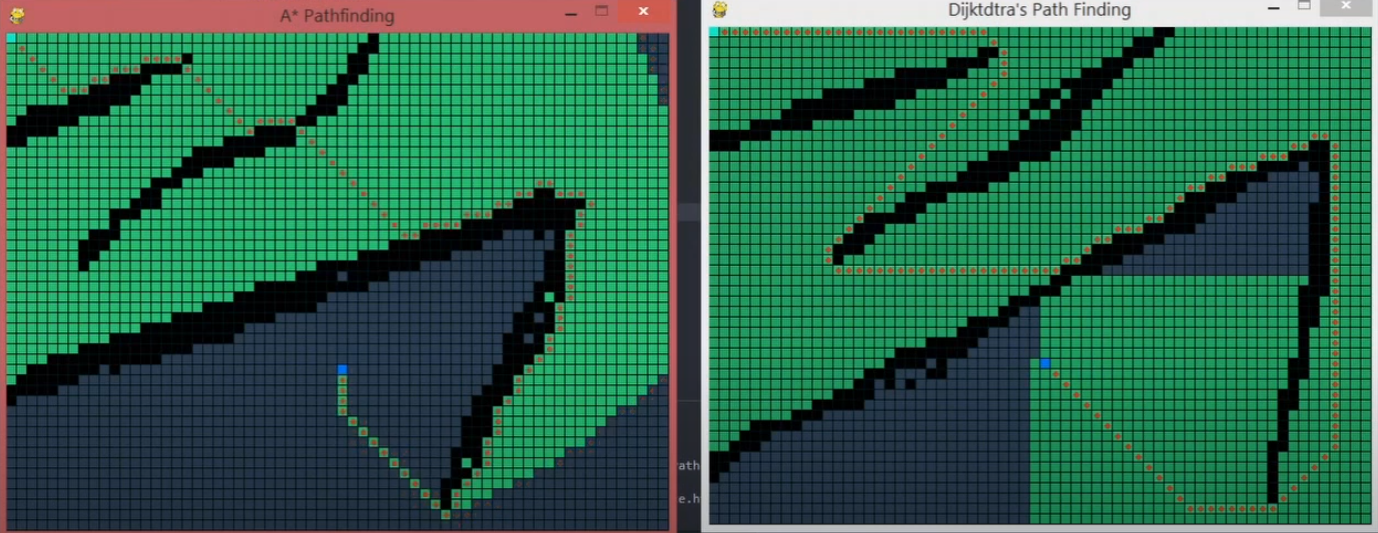
Figure 3.8.6 Path finding with obstacles