3.8.4. Topological Sort

TC: O(|V|+|E|) , SC: O(|E|)

Topological sort of a directed graph is a linear ordering of its vertices such that for every directed edge uv from vertex u to vertex v, u comes before v in the ordering.

We can use the Course Schedule question as an example. There are a total of n courses you have to take, labeled from 0 to n - 1. Some courses may have prerequisites, for example to take course 0 you have to first take course 1, which is expressed as a pair: [0,1]. Given the total number of courses and a list of prerequisite pairs, is it possible for you to finish all courses?

Example 1:
Input: 6, [[1,0],[2,1],[2,0],[3,2],[4,3],[5,3],[5,4]]
Output: true

Example 2:
Input: 2, [[1,0],[0,1]]
Output: false
Explanation: There are a total of 2 courses to take. To take course 1 you should have finished course 0, and to take course 0 you should also have finished course 1. So it is impossible.

0 -----> 2 -----> 3 -----> 4          0 -----> 2 -----> 3 -----> 4
 \      ^          \     /             \      ^          ^     /
  \    /            \   /               \    /            \   /
   v  /              v v                 v  /              \ v
    1                 5                   1                 5
topological sortable                  NOT topological sortable(cycle 3->4->5)

3.8.4.1. Post-order DFS

Post-order DFS will be faster than Kan’s Algo to find cycle. To find cycle, we track the color state of a node. Initially all the nodes are white color. When we enter the DFS function, we mark it as grey. When we back-track and unwind the stack, we mark it as black.

 1#include <gtest/gtest.h>
 2#include <sein.hpp>
 3
 4namespace ns_topo {
 5bool dfs_with_cycle_detection(vector<vector<int>> &graph, vector<int> &visit, int i) {
 6  if (visit[i] == -1) return false;
 7  if (visit[i] == 1) return true;
 8  visit[i] = -1;
 9  for (auto a: graph[i])
10    if (!dfs_with_cycle_detection(graph, visit, a)) return false;
11  visit[i] = 1;
12  return true;
13}
14
15bool canFinish_DFS(int numCourses, vector<pair<int, int>> prerequisites) {
16  vector<vector<int>> graph(numCourses);
17  vector<int> visit(numCourses);
18  for (auto [x, y]: prerequisites)
19    graph[y].push_back(x);
20  for (int i = 0; i < numCourses; ++i)
21    if (!dfs_with_cycle_detection(graph, visit, i)) return false;
22  return true;
23}
24}  // namespace ns_topo
25using namespace ns_topo;
26TEST(_topo_course_schedule_dfs, a) {
27  vector<pair<int, int>> pre = {{1, 0}, {2, 1}, {2, 0}, {3, 2}, {4, 3}, {5, 3}, {5, 4}};
28  EXPECT_TRUE(canFinish_DFS(6, pre));
29  pre[5] = {3, 5}; // add a cycle
30  EXPECT_FALSE(canFinish_DFS(6, pre));
31}

To get a topological sorted path:

 1// find one path by DFS
 2bool dfs_with_cycle_detection(vector<vector<int>> g, vector<int>& path, int i, vector<int>& color){
 3  if(color[i]==0) return false; // cycle detected
 4  if(color[i]==1) return true; // yes, no cycle!
 5  color[i]=0;
 6  for(int n: g[i])
 7    if (not dfs_with_cycle_detection(g,path,n, color)) return false;
 8  path.push_back(i), color[i]=1;
 9  return true;
10}
11vector<int> find_topo_order_dfs(int n, vector<pair<int, int>> pre) {
12  vector<vector<int>> G(n); // adjacency list
13  vector<int> r, color(n, -1), in(n);
14  for (auto [cur,pr]: pre) G[pr].push_back(cur), in[cur]++;
15  for (int i=0; i<n; i++) {
16    if (in[i]==0) {
17      if (not dfs_with_cycle_detection(G, r, i, color)) return {};
18    }
19  }
20  reverse(r.begin(), r.end());
21  return r;
22}

3.8.4.2. Kahn Algo - BFS with Zero-Degree Nodes

❤️ The advantage of Kahn’ algo is DAG checking is not needed.

Topologically sortable == No cycle!

 1#include <gtest/gtest.h>
 2#include <sein.hpp>
 3
 4namespace ns_topo {
 5bool canFinish_Kahn(int numCourses, vector<pair<int, int>> prerequisites) {
 6  unordered_map<int, set<int>> suc, pre;
 7  unordered_set<int> ns;
 8  for (auto [cur, pr]: prerequisites)
 9    suc[pr].insert(cur), pre[cur].insert(pr), ns.insert(pr);  // ns will include all nodes
10  for (auto p: pre) ns.erase(p.first);  // leave 0-in-degree in ns
11  while (!ns.empty()) {
12    unordered_set<int> tmp;
13    for (int i: ns) {
14      if (suc.count(i)) {
15        for (int j: suc[i]) {
16          if (pre.count(j) == 0) continue;  // in-degree==0
17          pre[j].erase(i);
18          if (pre[j].empty())
19            pre.erase(j), tmp.insert(j);
20        }
21        suc.erase(i);
22      }
23    }
24    ns = tmp;
25  }
26  return pre.empty() && suc.empty();
27}
28
29bool canFinish_BFS(int numCourses, vector<pair<int, int>> prerequisites) {
30  vector<vector<int>> graph(numCourses);
31  vector<int> in(numCourses);
32  for (auto [x, y]: prerequisites)
33    graph[y].push_back(x), ++in[x];
34  queue<int> q;
35  for (int i = 0; i < numCourses; ++i)
36    if (in[i] == 0) q.push(i);
37  while (!q.empty()) {
38    int t = q.front(); q.pop();
39    for (auto a: graph[t]) {
40      --in[a];
41      if (in[a] == 0) q.push(a);
42    }
43  }
44  for (int i = 0; i < numCourses; ++i)
45    if (in[i] != 0) return false;
46  return true;
47}
48}  // namespace ns_topo
49using namespace ns_topo;
50TEST(_topo_course_schedule_bfs, a) {
51  vector<pair<int, int>> pre = {{1, 0}, {2, 1}, {2, 0}, {3, 2}, {4, 3}, {5, 3}, {5, 4}};
52  EXPECT_TRUE(canFinish_Kahn(6, pre));
53  EXPECT_TRUE(canFinish_BFS(6, pre));
54  pre[5] = {3, 5}; // add a cycle
55  EXPECT_FALSE(canFinish_BFS(6, pre));
56}

To get a topological sorted path:

 1// find one path by BFS
 2vector<int> find_topo_order_bfs(int n, vector<pair<int, int>> pre) {
 3  vector<vector<int>> G(n); // adjacency list
 4  vector<int> in(n), res;
 5  for (auto [cur,pr]: pre) G[pr].push_back(cur), ++in[cur];
 6  queue<int> q0;  // enqueue all nodes with 0 in-degree
 7  for (int i = 0; i < n; ++i)
 8    if (in[i] == 0) q0.push(i);
 9  while (!q0.empty()) {
10    int t = q0.front(); q0.pop();
11    res.push_back(t);
12    for (int i: G[t])
13      if (--in[i] == 0) q0.push(i);
14  }
15  if (res.size() != n) return {};  // topologically un-sortable
16  return res;
17}

With BFS, we can get all possible topological paths. First, we get the Breadth First Tree (CLRS p600) with a layered BFS. Then we use DFS and permutation to get all the possible paths. Please be noted the algorithm here is different from combination algo here: https://leetcode.com/problems/letter-combinations-of-a-phone-number/.

 1// find all paths by BFS and Permutation
 2void permute_dfs(vector<int>& nums, vector<vector<int>>& r, vector<int>& p,vector<bool> vd)
 3{
 4  if (p.size() == nums.size()){r.push_back(p); return;}
 5  for(int i=0; i<nums.size(); ++i){
 6    if (vd[i]) continue;
 7    vd[i]=true, p.push_back(nums[i]);
 8    permute_dfs(nums,r,p,vd);
 9    p.pop_back(), vd[i] = false;// backtrack and unwind
10  }
11}
12
13vector<vector<int>> permute(vector<int>& nums) {
14  vector<vector<int>> r;
15  vector<int> p;
16  vector<bool> vd(nums.size()); // visited
17  permute_dfs(nums,r,p,vd);
18  return r;
19}
20
21void dfs(vector<vector<int>>& o, int n, int i, vector<int> p, vector<vector<int>>& fin){
22  if(o[i].empty()){
23    fin.push_back(p); return;
24  }
25  auto permus = permute(o[i]);
26  for(vector<int>& pm: permus){
27    auto t = p;
28    for(auto i: pm)
29      t.push_back(i);
30    dfs(o,n,i+1,t,fin);
31  }
32}
33
34vector<vector<int>> find_all_paths_bfs(int n, vector<pair<int, int>> pre) {
35  vector<vector<int>> G(n), tmp(n); // adjacency list
36  vector<int> in(n);
37  for (auto [cur,pr]: pre) G[pr].push_back(cur), ++in[cur];
38  queue<int> q0;  // enqueue all nodes with 0 in-degree
39  for (int i = 0; i < n; ++i)
40    if (in[i] == 0) q0.push(i);
41  int idx = 0, count=0;
42  while (!q0.empty()) {
43    int sz=q0.size();
44    while(sz--){
45      int t = q0.front(); q0.pop();
46      tmp[idx].push_back(t);
47      count++;
48      for (int i: G[t])
49        if (--in[i] == 0) q0.push(i);
50    }
51    idx++;
52  }
53  if (count != n) return {};  // topologically un-sortable, cycle detected
54  vector<int> p;
55  vector<vector<int>> res;
56  dfs(tmp,n,0,p,res);
57  return res;
58}
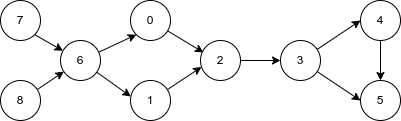
../_images/topo_simple.png

Figure 3.8.1 There are four different paths

 1TEST(_topo_get_one_path, a) {
 2  vector<pair<int, int>> pre = {{6,8}, {6,7}, {1,6}, {0,6}, {2, 1},
 3                                {2, 0}, {3, 2}, {4, 3}, {5, 3}, {5, 4}};
 4  vector<int> expected = { 7, 8, 6, 1, 0, 2, 3, 4, 5 };
 5  EXPECT_EQ(find_topo_order_bfs(9, pre), expected);
 6  expected = { 8, 7, 6, 0, 1, 2, 3, 4, 5 };
 7  EXPECT_EQ(find_topo_order_dfs(9, pre), expected);
 8  vector<vector<int>> all_expected = {
 9    {7, 8, 6, 1, 0, 2, 3, 4, 5},
10    {7, 8, 6, 0, 1, 2, 3, 4, 5},
11    {8, 7, 6, 1, 0, 2, 3, 4, 5},
12    {8, 7, 6, 0, 1, 2, 3, 4, 5},
13  };
14  auto all_paths = find_all_paths_bfs(9, pre);
15  EXPECT_EQ(all_paths, all_expected);
16  pre[5] = {3, 5}; // add a cycle
17  EXPECT_EQ(find_topo_order_bfs(9, pre), vector<int>({}));
18}