2.1.4. Sliding Window
Sliding window technique is used to solve subarray or substring problem. Rolling hash is basically a sliding window algorithm.
The window size could be fixed or variable.
2.1.4.1. Fixed Window
When it is fixed, after finding the window, we just need to move the head and tail index at the same time. The tricky part is from calculating statistics in the sliding window, eg, maximum, minimum, median.
Normally a special data structure is needed to solve fixed sliding window statistics problem.
2.1.4.1.1. Sliding Window Maximum
You are given an array of integers nums, there is a sliding window of size k which is moving from the very left of the array to the very right. You can only see the k numbers in the window. Each time the sliding window moves right by one position.
Return the max sliding window.
Example:
Input: nums = [1,3,2,5,8,7], k = 3
Output: [3,5,8,8]
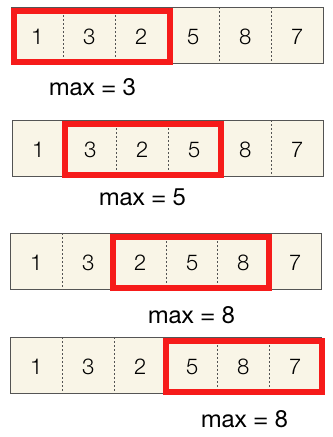
A monotonic decreasing queue can be used to solve this problem efficiently.
1class monotonic_queue {
2private:
3 deque<int> data;
4public:
5 void push(int n) {
6 while (!data.empty() && data.back() < n)
7 data.pop_back();
8 data.push_back(n);
9 }
10 int max() { return data.front(); }
11 void pop(int n) {
12 if (!data.empty() && data.front() == n)
13 data.pop_front();
14 }
15};
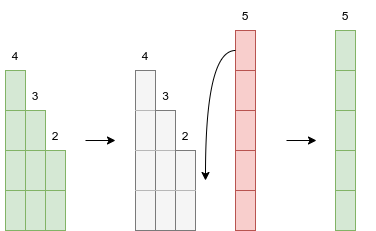
Figure 2.1.1 In a monotonic decreasing queue, a new item will evicts all the items less than itself. To insert 5 to [4,3,2], all the items are evicted and 5 is the only item after insertion.
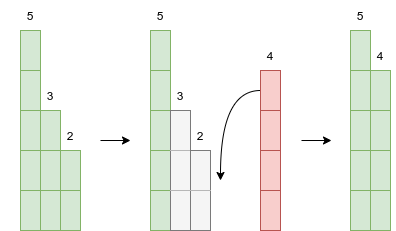
Figure 2.1.2 Insertion of 4 to [5,3,2] will evict 3 and 2, so the resulting queue becomes [5,4].
1vector<int> maxSlidingWindow(vector<int>& nums, int k) {
2 monotonic_queue window;
3 vector<int> res;
4 for (int i = 0; i < nums.size(); i++) {
5 if (i < k - 1) { // fill the first k-1 of the window first
6 window.push(nums[i]);
7 } else { // window slide forward
8 window.push(nums[i]);
9 res.push_back(window.max());
10 window.pop(nums[i - k + 1]);
11 }
12 }
13 return res;
14}
deque is needed because we need pop from front and back of the sequential data strucutre.
2.1.4.1.2. Sliding Window Meidan
A multiset can be used to solve this problem efficiently. Refer to Section 2.6.2 for multiset.
Window position Median
--------------- -----
[1 3 -1] -3 5 3 6 7 1
1 [3 -1 -3] 5 3 6 7 -1
1 3 [-1 -3 5] 3 6 7 -1
1 3 -1 [-3 5 3] 6 7 3
1 3 -1 -3 [5 3 6] 7 5
1 3 -1 -3 5 [3 6 7] 6
1vector<double> medianSlidingWindow(vector<int> nums, int k) {
2 multiset<int> window(nums.begin(), nums.begin() + k);
3 auto mid = next(window.begin(), k / 2);
4 vector<double> medians;
5 for (int i = k;; i++) {
6 medians.push_back((double(*mid) + *prev(mid, 1 - k % 2)) / 2);
7 if (i == nums.size()) // 💣
8 return medians;
9 window.insert(nums[i]);
10 if (nums[i] < *mid) mid--;
11 if (nums[i - k] <= *mid) mid++;
12 window.erase(window.find(nums[i - k])); // 💣
13 }
14}
Line 12 is to delete one number by value in a multimap.
2.1.4.2. Variable Window
The execution of a variable window size problem is a bit more tricky and will require more variables to keep track of where our window begins and ends.
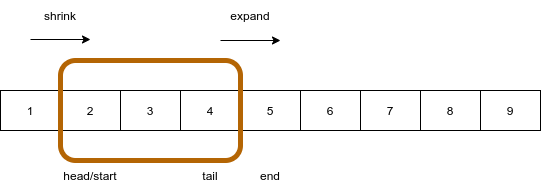
Figure 2.1.3 Sliding Window Technique
Sliding window characteristics:
Sliding window has a start(head) and end(tail)
Sliding window has status that indicate the status of the window
Sliding window grows/shrink toward one direction
Sliding window application principles:
Sliding window skipped some combinations to improve efficiency, to use sliding window needs to prove these combinations can be skipped.
In terms of implementation, here is the key ideas:
Use nested loop to move window: outer loop to expand the window, inner loop to shrink the window
The outer loop stop condition is the right boundary meets array end
The inner loop stop condition is the status of the window meets requirement, as long as it still meets requirement, shrink the window as possible.
The abstract idea of sliding window algorithm is:
int left = 0, right = 0;
while (right < s.size()) {
window.add(s[right]);
while (valid) {
window.remove(s[left]);
left++;
}
right++;
}
The data type of the window can vary depending on the situation, such as using the hash table as the counter, or you can use an array to do the same, since we only deal with English letters.
The slightly tricky part is the valid condition, and we might have to write a lot of code to get this updated in real time.
2.1.4.2.1. Find All Anagrams in a String
Given two strings s and p, return an array of all the substrings of s which are p’s anagram. You may return the answer in any order.
An Anagram is a word or phrase formed by rearranging the letters of a different word or phrase, typically using all the original letters exactly once.
This is a fixed-length sliding window problem, so we need to move the head and tail of the window at the same time.
1struct fmaq {
2 int m[256] = {};
3 bool n[256] = {};
4 int c = 0;
5 explicit fmaq(const string &p) {
6 c = p.size();
7 for (char ch : p) {
8 m[ch]++;
9 }
10 }
11 bool found() { return c == 0; }
12 void incr(char ch) {
13 m[ch]++;
14 if (m[ch] > 0) c++;
15 }
16 void decr(char ch) {
17 if (m[ch] > 0) c--;
18 m[ch]--;
19 }
20};
21
22// fixed-length window moving
23vector<string> get_all_anagrams(const string &s, const string &p) {
24 vector<string> r;
25 fmaq fm(p);
26 int L = s.size();
27 for (int i = 0, j = 0; i < L and j < L; j++) {
28 fm.decr(s[j]);
29 if (fm.found()) {
30 r.push_back(s.substr(i, j - i + 1));
31 }
32 if (j - i + 1 == p.size()) {
33 fm.incr(s[i]);
34 i++;
35 }
36 }
37 return r;
38}
2.1.4.2.2. Minimum Window Substring
Given a string S and a string T, find the minimum substring in S which will contain all the characters in T in complexity O(n).
For example, S = “ADOBECODEBANC”, T = “ABC” Minimum substring is “BANC”.
Note: If there is no such substring in S that covers all characters in T, return the empty string “”. If there are multiple such substrings, you can return any one of them.
Brute force way is to find all the substrings and find the shortest one which meets the requirement. The time complexity will be O(N^3).
To get O(N) time complexity, we can use sliding window. The first challenge for this problem is how to determine if the substring is valid. The second is how to move the pointers to find the next valid substring.
With a special mapping data structure, the problem becomes more clear.
1struct fmap { // frequency map with counter
2 int m[256] = {}; // dynamic
3 bool n[156] = {}; // static
4 int count = 0;
5 explicit fmap(const string& t) {
6 for (char c : t) {
7 if (m[c] == 0) {
8 count++, n[c] = true;
9 }
10 m[c]++;
11 }
12 }
13 bool invalid_char(char c) { return !n[c]; }
14 bool found() { return count == 0; } // found a valid substring
15 void decr(char c) {
16 m[c]--;
17 if (m[c] == 0) count--;
18 }
19 void incr(char c) {
20 if (m[c] == 0) count++;
21 m[c]++;
22 }
23};
The sliding window algorithm is basically a two-pointer algorithm. First we find the beginning position of a valid substring, then we expand the ending position.
1string minWindow(string s, string t) {
2 fmap cnt(t);
3 int j = 0, mi = INT_MAX, begin_ = 0;
4 for (int i = 0; i < s.size() and j < s.size(); i++) {
5 if (cnt.invalid_char(s[i])) {
6 continue;
7 }
8 while (!cnt.found() and j < s.size()) {
9 cnt.decr(s[j]);
10 j++;
11 }
12 if (cnt.found() and j - i < mi) {
13 mi = j - i, begin_ = i;
14 }
15 cnt.incr(s[i]);
16 }
17 return s.substr(begin_, mi);
18}
Test cases:
1 EXPECT_EQ(minWindow("ADOBECODEBANC", "ABC"), "BANC");
2 EXPECT_EQ(minWindow("bacbbaxcca", "aab"), "acbba");
2.1.4.2.3. Longest Substring with At Most Two Distinct Characters
1 struct fmap{
2 int m[256]={};
3 bool n[256]={};
4 int c=0;
5 bool should_expand(){
6 return c<=2;
7 }
8 void incr(char ch){
9 m[ch]++;
10 if (m[ch]==1) c++;
11 }
12 void decr(char ch){
13 m[ch]--;
14 if (m[ch]==0) c--;
15 }
16 int begin, mx=INT_MIN;
17 };
18
19 // "eceba" -> "ece"
20 string longest_substr_distinct_chars(const string& s){
21 fmap fm;
22 for(int i=0, j=0;i<s.size() and j<s.size();j++){
23 fm.incr(s[j]);
24 if(!fm.should_expand()){
25 fm.decr(s[i]);
26 i++;
27 }
28 if(fm.mx<j-i+1){
29 fm.mx = j-i+1, fm.begin=i;
30 }
31 }
32 if (fm.mx==INT_MIN)
33 return s;
34 return s.substr(fm.begin, fm.mx);
35 }
2.1.4.2.4. Longest Substring Without Repeating Characters
1 struct fmap{
2 int m[256]={};
3 bool n[256]={};
4 int c=0;
5 bool should_expand(int sz){
6 return c==sz;
7 }
8 void incr(char ch){
9 m[ch]++;
10 if (m[ch]==1) c++;
11 }
12 void decr(char ch){
13 m[ch]--;
14 if (m[ch]==0) c--;
15 }
16 int begin, mx=INT_MIN;
17 };
18
19 string longest_substr_unique_chars(const string& s){
20 fmap fm;
21 for(int i=0, j=0;i<s.size() and j<s.size();j++){
22 fm.incr(s[j]);
23 if(!fm.should_expand(j-i+1)){
24 fm.decr(s[i]);
25 i++;
26 }
27 if(fm.mx<j-i+1){
28 fm.mx = j-i+1, fm.begin=i;
29 }
30 }
31 if (fm.mx==INT_MIN)
32 return s;
33 return s.substr(fm.begin, fm.mx);
34 }
Dynamic minimum subarray query could be efficiently solved by segment tree. It will be covered later at Section 3.3.3.1.